X and the City: Modeling Aspects of Urban Life (39 page)

We will just calculate the mean lengths of parallel roads in circular and rectangular town centers as we move from one side of the town center to the other. Even this rather crude approach yields answers close to those found in the literature, indicating that the coefficient is relatively insensitive to the structure of the road network. First, we consider a set of N-S parallel roads in a circular town center of radius
r
(see
Figure 14.1
), separated by a constant distance
r
/
n
, where
n
is a positive integer. In so doing, we are neglecting the combined width of the road network compared with the town center area. Each road passing within a distance
pr
/
n
of the origin (where
p
is an integer less than
n
) has length 2
r
[1 − (
p
/
n
)
²
]
^1/2
, and for each
p
> 0 there are two roads of identical length. There are 2(
n
− 1) + 1 = 2
n
− 1 roads, so the discrete average length is given by

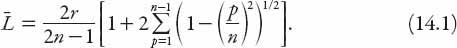
Of course, an identical result holds for W-E roads, and the combined average will be the same. To express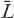
in terms of
A
^1/2
we merely write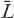
=
kA
^1/2
=
kπ
^1/2
r
, so that the coefficient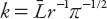
. For
n
= 3 (five roads),
k
≈ 0.99; for
n
= 4 (seven roads),
k
≈ 0.96, and for
n
= 10 (nineteen roads),
k
≈ 0.92. Thus we see that these constants are well within the range found by Smeed.

Figure 14.1. Cartesian road “grids” in rectangular (shown here, square) and circular cities.

It may be of some interest to take the mathematical limit as
n
→ ∞, in the above equation and calculate the average length for a continuum of roads—perhaps more appropriate for ducks on a circular pond (though possibly a good description of the morning commute!). In practice, it is less messy just to set up the integral for the average value of the function
L
(
x
) = 2(
r
²
−
x
²
)
^1/2
, that is,

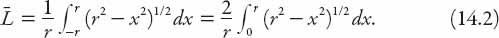
This is a standard integral, and can be evaluated with a trigonometric substitution to find that

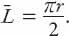
Hence, proceeding as before, setting
πr
/2 =
kA
^1/2
yields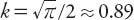
. It would appear that this is indeed the limit of the decreasing sequence of
k
-values suggested by equation (14.1).

Exercise:
(a) Verify this result for
; (
b
) find
k
for
n
= 100.

Now we proceed to evaluate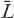
and
k
for a rectangular town center. We suppose that the longer sides are parallel to the
x
-direction, for convenience. The sides are of length
a
, and
b
>
a
. There are
n
+ 1 N-S equally spaced roads (including the sides) and, similarly,
m
+ 1 W-E equally spaced roads. We assume the N-S and W-E road spacing is the same, Δ, say. The average distance traveled (again, from side to opposite side, for simplicity) is