X and the City: Modeling Aspects of Urban Life (67 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

And now, to geometry!
r
max
: “CIGARS AND APPLES” IN THE CITY
An important theorem in plane geometry states that the angle subtended by a chord (
CE
) at the center of a circle (2
α
) is twice that subtended at any point (
F
) on the circumference. This is easily established from
Figure 22.2
by adding the radius
OF
to form three isosceles triangles, and noting that the sum of the angles around
O
must be 360°. Now let
C
represent a light source, and
E
represent the observer’s eye. If the volume of space surrounding the observer and source contains either raindrops or hexagonal ice crystals (and is sufficiently large), then for raindrops,
α
≈ 42° and the arc
CFE
is the locus of all raindrops in that plane scattering light into the observer’s eye. But by symmetry this is also true for all rotations of that arc around the line
CE
, forming, as it turns out, an apple-shaped surface. For reasons that will become obvious below, this surface is known as “Minnaert’s cigar.”
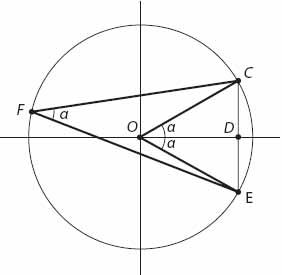
Figure 22.2. Angle subtended by a chord (
CE
) at the center of a circle (2
α
) is twice that subtended at any point (
F
) on the circumference.
Reference has already been made to Marcel Minnaert, the author of a famous and widely quoted book
Light and Colour in the Open Air
[
38
]. In that book (pp. 206–207) he made the following observation:
One very cold evening (17° F) beautiful halo phenomena could be seen in the steam from a train in the railway station. Near one of the lamps, where the cloud of steam was blown in every direction, a cigar-shaped surface of light could be seen, having one end near the eye, the other near the lamp; all little crystals traversing this surface were lit up, but the space inside was quite dark; the cone tangential to the surface had an angle at the vertex of about 44°. It is at once clear that the cigar-shaped surface is simply the locus of all those points P such that the sum of the angles subtended by EP and PL at L and E respectively is 22°.
Minnaert then goes on to note that the remarkable three-dimensional nature of this observation is only possible because (i) the light source is so near the eyes, and (ii) of the stereoscopic effects associated with both eyes viewing the crystals (see
Figure 22.3
).
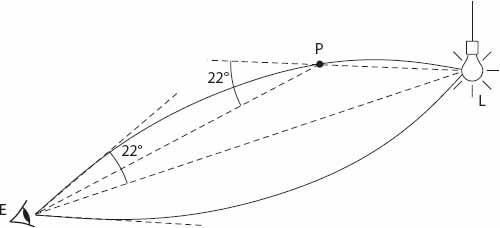
Figure 22.3. Sketch of “Minnaert’s cigar” (Redrawn from Minnaert 1954).

Figure 22.4. Minnaert”s cigar for the 22° halo, illustrating the three-dimensional form (Redrawn from Mattsson et al. 2000).
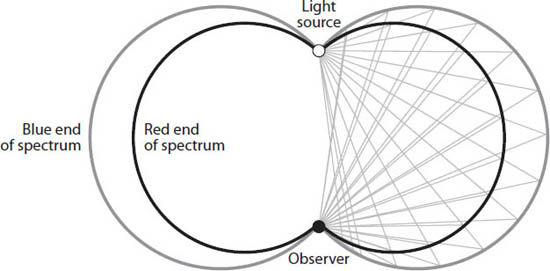
Figure 22.5. Minnaert’s “apple-shaped cigar” for the 22° halo, generated by rotating the larger arc around the chord
CE
in
Figure 22.2
(or chord
LO
in
Figure 22.6
). The light source is at the top of the “core” and the observer”s eye is at the bottom. It is drawn for both the red and blue ends of the visible spectrum. Redrawn from a diagram by Christian Fenn (see [
39
]).
Figure 22.4
is a perspective rendering of the Minnaert 22° cigar, a spindle–shaped surface, truncated here to emphasize its three-dimensional nature. And the apple-shaped surface in
Figure 22.5
is also referred to as Minnaert’s cigar (even though it looks like no cigar I’ve ever seen!). It arises from rotating the smaller arc
CE
about the chord in
Figure 22.2
, and the apple surface arises from rotating the larger arc
CFE
about the same chord.
In fact there are several other intermediate surface shapes that can arise from similar considerations. In addition to the “classical” 22° cigar halo surface (with supplementary angle 158°), there is a less common 46° one (with supplementary angle 134°). Furthermore, as also noted in
Appendix 11
, there is a secondary rainbow which can appear at an angle of 51° from the anti-solar direction (or as a circle of angular radius 129° around the sun). When rotated about the corresponding chord
LO
(see
Figure 22.6
, where the segments
LO
correspond to the chord
CE
in
Figure 22.2
), the appropriate “cigar surfaces” are generated (
Figures 22.4
and
22.7
). In each case, the vertex angles marked in
Figure 22.6
are the angles measured from the anti-solar direction. The scattering angle—the angle through which light from the source has been deviated—is the supplement of these, thus 22° and 46° for the halo surfaces, 138° and 129° for the rainbow surfaces.
An enlarged version of the small 22° “cigar” surface of
Figure 22.6
is shown in
Figure 22.7
; as in
Figure 22.4
it can be interpreted as a surface of revolution.
The detailed geometry of the situation is governed by
Figure 22.8
, where the observer’s eye is at
B
and the light source is at
D
. We see from triangle
BCD
that
r
c
+
r
d
=
r
max
. From this it follows that
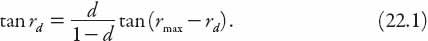
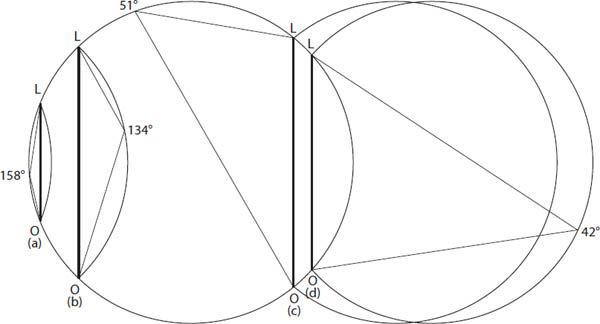
Figure 22.6. Generalization of Minnaert”s cigar for (a) the 22° halo, (b) the 46° halo, (c) the secondary rainbow, and (d) the primary bow. The light source is at
L
and the observer”s eye is at
O
. The angles stated are measured from the “anti-source” point (as in the daylight anti-solar point). Thus the supplement of the 22° halo angle is 158°, etc. (Based on Figure 1 in Mattsson and Barring, 2001).
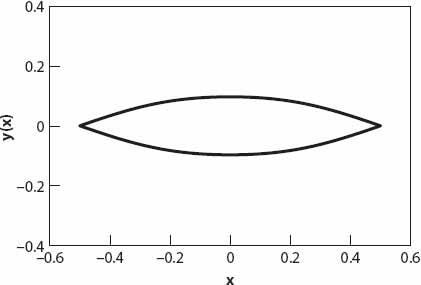
Figure 22.7. Profile of Minnaert’s cigar as defined by equation (22.5).
First, we do a little geometry. The unit of length is taken as the distance
BD
, that is,
BD
= 1. This is the length of the “cigar.” The radius of the circle is
R
=
BD
/(2 sin
r
max
) = (2 sin
r
max
)
−1
; the distance
d
c
=
BC
between the crystals scattering light into the observer’s eye and his eye at
B
is

