X and the City: Modeling Aspects of Urban Life (37 page)

Figure 13.1.
v
₁
and
v
₂
in mph vs.
N
(cars/hr/highway width in ft)

Of course, not all vehicles will be cars. In some of the literature [
20
]–[
27
], bicycles were regarded as the equivalent of one third of a car, buses the equivalent of three cars, and so forth. Thus, in order to achieve a speed of
v
mph, equation (13.1) suggests that each car on the road, during a period of one hour, requires a width of (68 − 0.13
v
²
)
⁻¹
ft. A bus would require three times this width and a bicycle one third (a motorcycle, presumably, one half).

X
=
δT
: Question:
How are increases in traffic and losses in time (due to congestion) related?

As above, we’ll write
N
(
v
) as a quadratic function,

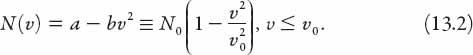
where
N
₀
=
a
and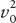
=
a/b
.
N
₀
is interpreted as the maximum flow of vehicles and
v
₀
as the speed under “light” traffic conditions. Suppose that a journey is of distance
l
and we define
T
, the accumulated time loss due to congestion, as the difference (for
N
vehicles) between the times traveled at speeds
v
and
v
₀
, respectively, then

We shall define the relationship between small changes in
T
and
N
(
δT
and
δN
respectively) by

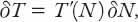
where
T
′(
N
) is the derivative of
T
with respect to
N
. If
T
′ is not too large, a small change in
N
induces a correspondingly small change in
T
according to this formula. This is a slight variation on the definition of differentials in elementary calculus, but it will be quite sufficient an approximation for our
purposes, and indeed a good one, so we will use “=” rather than “≈” in what follows. From equations (13.2) and (13.3) we obtain

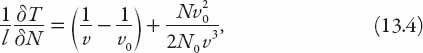
or

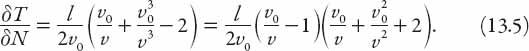
As a function of the ratio
v
₀
/
v
, the right-hand side of (13.5) is a cubic polynomial, increasing monotonically from zero when the traffic is light (
v
₀
/
v
= 1). Graphically, it is perhaps easier to appreciate as a function of the ratio of speed to the “light” speed (not the speed of light!), that is, in terms of
x
=
v
/
v
₀
. Thus

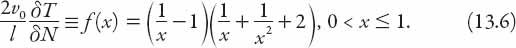
The graph of this decreases monotonically to zero when
x
= 1, and as can be seen in
Figure 13.2
, the congestion term on the left of equation (13.6) decreases by a factor of about twelve as
x
increases from 0.2 to 0.5; that is, when the average speed is one fifth of the speed of light traffic, the time loss is about twelve times as great as when the average speed is one half that of light traffic. Furthermore, from equations (13.2), (13.3), and (13.5) we can deduce an expression for the following useful measure of congestion:

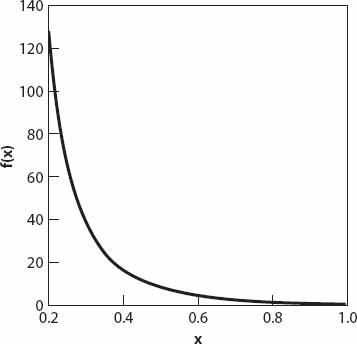
Figure 13.2. Graph of the function
f
(
x
) defined by equation (13.6).

Clearly
δT
/
T
increases as a quadratic function of the percentage increase of traffic.

X
=
δt
: Question:
What difference will just one more vehicle make?

The change in time for a journey of length
l
and duration
t
=
l
/
v
when there is a small change
δv
in speed is given by
δt
= −
lδv
/
v
²
. If this change arises because of a small change
δN
in the traffic flow, we may write