X and the City: Modeling Aspects of Urban Life (35 page)

This explains the shape of the graph near the origin; as
K
→ 0
⁺
,
Q
′(
K
) → ∞ (as does
q
′(
k
) of course). As the concentration goes to zero, any interaction between vehicles will become negligible, and the flow would become an average “free speed,” which renders this car-following model inapplicable. In practice, the real flow at any concentration is probably less than this, so the slope of the graph near the origin will not be so steep (see
Figure 10.1
).

In closing this section, let us revisit equation (12.5) for the capacity
q
_max
. In terms of the original parameters (see equation (12.1))

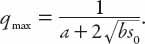
It is clear from this formula that the capacity can be raised by decreasing the reaction time (a), decreasing the headway distance (
s
₀
), or increasing the desired maximum deceleration (
b
⁻¹
) (not a good idea), or indeed, any combination of these changes. Conversely, the capacity will be lowered by changing them in the opposite directions.

It is appropriate to mention an “equation” from the field of psychology in this context, namely “
Response
=
Sensitivity
×
Stimulus
.” The response is usually identified as the acceleration (or deceleration) of the following vehicle, and experimental studies have shown that there is a high correlation between a driver’s response and the relative speed of the vehicle ahead—the stimulus. With this in mind, note that differentiation of equation (12.1) with respect to
t
yields

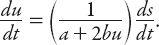
This is a type of stimulus-response equation, although the sensitivity term (
a
+ 2
bu
)
⁻¹
decreases with increasing speed
u
, so it is not a particularly useful interpretation in this regard.

There is another avenue worth pursuing in connection with the reaction time
T
. If we define
s
_n
=
x
_n
−1
−
x
_n
as the spacing ahead of the
n
th car (at location
x
_n
), rewrite equation (11.3) in terms of the discrete speed
u
_n
=
dx
_n
/
dt
, and let
t
→
t
−
T
, this equation becomes (with
c
_n
= 0)

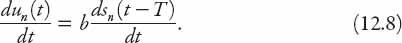
This differential-difference can be solved exactly using more advanced techniques, but we will use an approximate method consistent with the level of this book. We can expand the right-hand side of this equation as a Taylor series about
t
; retaining up to the quadratic term in
T
we obtain the expression

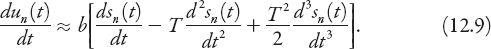
Now

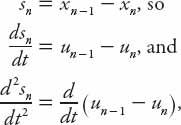
and so on. Placing all the terms involving
u
_n
on the left-hand side, and all those in
u
_n
−1
on the right, we have the following constant coefficient second-order nonhomogeneous ordinary differential equation (quite a mouthful):

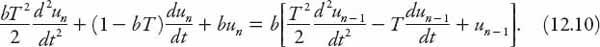
If we know the speed of vehicle (
n
− 1), this equation enables us in principle to find the speed of the following vehicle (
n
). From the elementary theory of differential equations we know that the general solution of this equation is the sum of the solution to the homogeneous equation (i.e., with zero right-hand side) and a particular solution to the complete equation (with the right-hand side being a known function of
t
). The former solution is the most important determinant of the
instability
of the traffic flow, so we seek solutions of
equation (12.10) in the form
u
_n
(
t
) =
Ue
^pt
, where
U
is a constant. There are two values of the constant
p
to be found by substitution. These values are roots of the quadratic equation

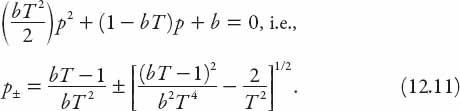
The nature of
p
(and hence the solution) depends on the sign of the radicand; it will be real (and hence non-oscillatory), provided

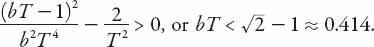
Otherwise the roots are complex conjugates, and the sign of the real part determines the solution behavior. If

(i) 0 ≤
bT
≤
− 1; both roots are negative and the solution is exponentially decreasing (stable).

 (ii)
− 1 <
bT
< 1; both roots are complex, and the solution is damped oscillatory (stable).