X and the City: Modeling Aspects of Urban Life (16 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

It is important to note that rain is a “stream” of discrete droplets, not a continuous flow. It is reasonable to define a measure of rain intensity by comparing the rate at which rain is falling with the speed of the rain. The speed of raindrops depends on their size. At sea level, a very large raindrop about 5 millimeters across falls at the rate of about 9 m/s (see
Chapter 25
for an unusual way to estimate the speed of raindrops). Drizzle drops (less than 0.5 mm across) fall at about 2 meters per second. We shall use 5 m/s (or 500 × 3600 = 1.8 × 10
6
cm/hr) as an average value. The ratio of the precipitation rate to the rain speed [
13
] is called the rain intensity,
I
. For the figures used here,
I
= 2/(1.8 × 10
6
) ≈ 1.1 × 10
−6
. Therefore
I
is a parameter:
I
= 1 corresponds to continuous flow (at that speed), whereas
I
= 0 means the rain has stopped, of course!
If as in
Figure 6.2
the rain is falling with speed
c
m/s at an angle
θ
to the vertical direction, and you are running into it, the vertical (downward) component of speed is
c
cos
θ
and the relative speed of the horizontal component is
c
sin
θ
+
v
. And if you move fast enough, only the top and front of you will get wet. For now let’s assume this is the case. Since you are
not
in fact a thin sheet (your head does get wet), we will model your shape as a rectangular box of height
l
, width
w
and thickness
t
(all in m). The “top” surface area is
wt
m
2
, and the volume of rain is “collected” at a rate
R
= intensity × surface area × rain speed =
Iwtc
cos
θ
, expressed in units of m
3
/s. In time
d
/
v
the amount collected is then
Iwtdc
cos
θ
/
v
m
3
. A similar argument for the front surface area gives
Iwld
(
c
sin
θ
+
v
)/
v
m
3
, resulting in a total amount
T
of rain collected as
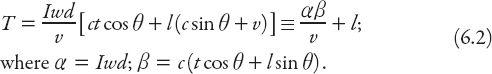
Before putting some numbers into this, note that if
θ
were the only variable in this expression, then
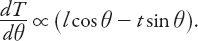
Because this vanishes at
θ
= arctan(
l
/
t
) and
d
2
T
/
dθ
2
< 0 there, this represents a
maximum
accumulation of rain. Physically this means that you are running almost directly into the rain, but the relative areas of your top and front are such that the maximum accumulation occurs when it is (in this case) not quite
horizontal. In addition, of
v
were the only variable, then
dT
/
dv
= −
αβ
/
v
2
< 0 if
β
> 0, so that
T
decreases with speed
v
if tan
θ
> −
t
/
l
. If tan
θ
< −
t
/
l
, then
T increases
with speed. This corresponds to more and more negative values of
θ
, that is, the rain is coming from behind the runner.
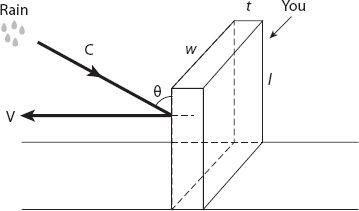
Figure 6.2. Configuration for a rectangular box-person running in the rain.
Let’s put some meat on these bones, so to speak. Suppose that the rectangular box has dimensions
l
= 1.5 m,
w
= 0.5 m, and
t
= 0.2 m. Furthermore, we have chosen
v
= 6 m/s (about 13 mph); and
c
= 5 m/s. Substituting all these values into expression (6.2) for
T
we obtain
T
≈ 4.6 × 10
−2
(9 + cos
θ
+ 7.5 sin
θ
) liters. It is readily confirmed that this has a maximum value of about 0.76 liters when
θ
≈ 82.4°. A graph of
T
(
θ
) is shown in
Figure 6.3
for −
π
/2 <
θ
<
π
/2. Note also that for a given speed when
θ
< 0 (i.e., the rain is coming from behind you) the quantity of rain accumulated is smaller (as would be expected) than when you are running into the rain. Notice also the wide range of values, from a high of just below 0.8 liters to a low of less than 0.1 liters when the rain is hitting you horizontally from behind!
We need to be a little more careful with the case of
θ
< 0 because (6.2) could become negative (and therefore meaningless) for some parameter ranges. If we replace
θ
by −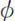 ,
,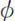 > 0, then this equation becomes
> 0, then this equation becomes
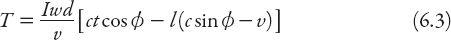
This is negative if

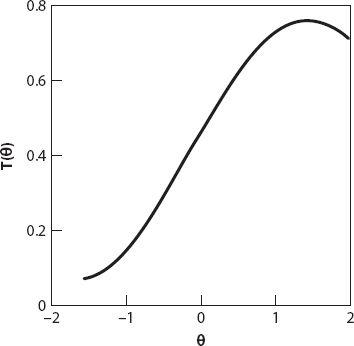
Figure 6.3. Total amount of rain captured as a function of rain angle (radians).
Note that this can never happen if
v
≥
c
, and will not for the choice of
v
and
c
made here (
v
/
c
= 1.2). If the inequality (6.4)
is
satisfied, the “offending term” comes from the “front accumulation” value