X and the City: Modeling Aspects of Urban Life (23 page)

from which follow the speed and displacement equations

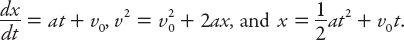
We have chosen
x
(0) = 0. In order to stop before the intersection in at most
T
seconds, it follows from the second of these equations that

On the other hand, to continue through, we note that the vehicle must travel a distance
d
₀
+
s
in less than
T
, so that requiring
x
(
T
) ≥
d
₀
+
s
in the third equation above yields the inequality

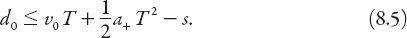
In each inequality, we have assumed that the maximum deceleration and acceleration are applied accordingly. Before treating the inequalities graphically, we write them in dimensionless form. This will reduce the number of parameters needed from five to four. To illustrate this, if we divide the distance
d
₀
by
s
, we obtain a dimensionless measure of distance in units of
s
, namely
δ
=
d
₀
/
s
. Similarly, we define dimensionless speed by
σ
=
v
₀
/(
s
/
T
), time by
τ
=
t/T
, and
acceleration by
α
_±
=
a
_±
/(
s
/
T
²
). Notice that
τ
is a measure of time in units of the yellow light duration. In these new units, the combined inequalities show that a driver may successfully choose either legal alternative provided that

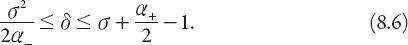
Now we are in a position to discuss reasonable ranges on these parameters, starting with the physical data. Typical ranges have been taken from the literature [
17
]. If we adopt the range for the speed approaching the intersection as 10 mph ≤
v
₀
≤ 70 mph (or approximately 15 fps ≤
v
₀
≤ 100 fps), with the bounds 20 ft ≤
d
₀
≤ 600 ft, 30 ft ≤
s
≤ 100 ft, 2 s ≤
T
≤ 6 s, and 3 ft/s
²
≤ |
a
_±
| ≤ 10 ft/s
²
, then we find that 0.3 ≤
σ
≤ 16.7, 0.2 ≤
δ
≤ 20, and 0.12 ≤
α
_±
≤ 8.3. Since we are measuring time in units of
T
, the results are relative, even though
T
itself can and does vary. In
Figure 8.1
we plot a generic graph for the bounds on
δ
(
σ
) (based on equation (8.6)). There are four regions to consider. The region
OAB
corresponds to a domain with relatively low speed and small distance, and represents a portion of (
σ
,
δ
) space for which either option—stop or continue—is viable. Continuing, the region above
ABC
is a (theoretically infinite!) region with relatively low speed and large distance, so it is easy to stop before reaching the intersection.
BCD
is a region with relatively high speed and large distance, and represents a domain in which a violation (or accident) is likely. Finally, below
OBD
the region corresponds to relatively high speed and small distance, implying it is possible to continue through the intersection before the light turns red.

The various
δ
_i
(
σ
) functions chosen here (with
i
= 1, 2, 3, 4, also based on equation (8.6)) are defined as follows:

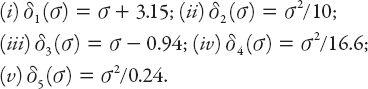
As in
Figure 8.1
,
Figure 8.2
shows dimensionless position/speed graphs identifying regions of safety. Obviously this is a simplistic analysis of the stop-light problem; an experienced and careful driver will have developed some measure of intuition (and caution) concerning whether a successful “continue through” is possible. We have not considered the possibility of skids; they are likely to occur if the deceleration is too large, and poor road conditions (wet, icy, etc.) will greatly affect the required stopping distance. In addressing this problem, Seifert (1962) has suggested posting signs along the roadside indicating a speed at which it is safe to continue through or stop from that location. It’s a thought!

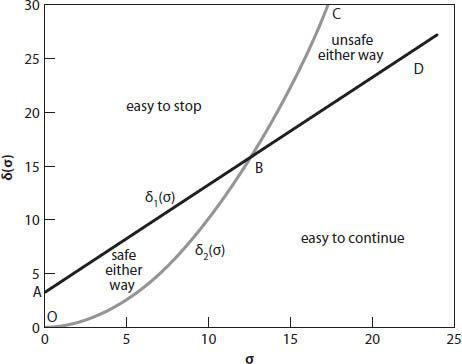
Figure 8.1. Dimensionless distance-speed graphs indicating regions of legal/illegal options based on equation (8.6);
δ
₁
(
σ
) =
σ
+ 3.15 and
δ
₂
(
σ
) =
σ
²
/10.

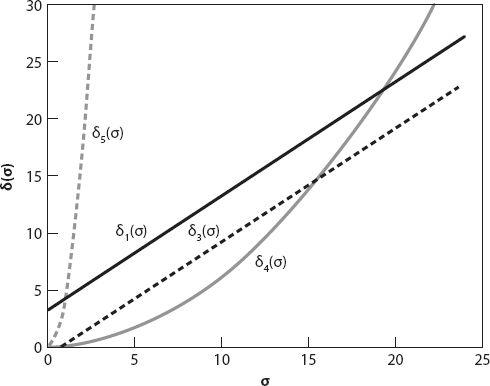
Figure 8.2. Additional dimensionless distance-speed graphs based on equation (8.6) (see
Figure 8.1
). Here
δ
₁
is as in
Figure 8.1
, and
δ
₃
(
σ
) =
σ
− 0.94;
δ
₄
(
σ
) =
σ
²
/16.6; and
δ
₅
(
σ
) =
σ
²
/0.24.

Should the driver of a car try to stop or turn in order to avoid a collision? We shall examine this question for several different situations, the first being when a car approaches a T-intersection with a brick wall directly ahead across the intersection. We shall assume that the junction is free of other vehicles, so the only possibility of collision involves the car hitting the wall. Furthermore, we shall assume that there is no skidding, in which case the coefficient of friction in a turn may be considered to be the same as that in the forward direction. (Skidding would involve the coefficient of
sliding
friction, in general different from that for rolling friction.)

We can examine three possible choices [
18
] as illustrated in
Figure 8.3
: (i) to steer straight ahead and apply the brakes for maximum deceleration; (ii) to turn in a circular arc without braking (using all the available force for centripetal acceleration); or (iii) to choose some combination of (i) or (ii), such as turning first and then steering straight (or vice versa), or even steering in a spiral path. In fact, option (ii) can be ruled out immediately by means of a simple (but nontrivial) argument as follows.

Suppose that the distance of the car from the wall is
l
and that its speed at that point is
v
₀
. The force required to turn the vehicle (of mass
m
) in a circular arc of radius
l
is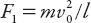
, but the force required to bring the vehicle to stop in a distance
l
is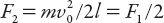
. This means that if the car can be turned without hitting the wall, it can be brought to a stop halfway to the wall. Regarding option (iii), a rather more subtle argument [
18
] shows that the appropriate choice is still to stop in the direction of motion. Apart from a brief discussion below, this will not be elaborated on here; instead we shall examine some other potential driving hazards. It should be no surprise that the worst highway accidents are those involving head-on collisions.