X and the City: Modeling Aspects of Urban Life (59 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam


where
x
0
is the location of this particular electron on the
x
-axis,
E
0
is the amplitude of the wave, and
ω
= 2
π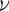 is called the angular frequency of the wave. As the wave passes, electrons will be accelerated back and forth in the
is called the angular frequency of the wave. As the wave passes, electrons will be accelerated back and forth in the
z
-direction, which in turn will radiate electromagnetic waves—this radiation is the scattered light. An important consequence of our assumption that the particle is small is this: since
R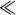 λ
λ
the electric field is almost uniform throughout the particle, so every electron (with charge
e
) experiences close to the same force (
eE
) accelerating it, proportional to its displacement
s
from its former position of equilibrium in the absence of the wave. The force will always be such as to move the electron back toward that position, so it can be incorporated in Newton’s second law of motion as follows:
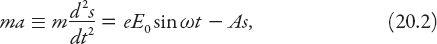
m
being the electron mass,
a
being its acceleration, and
A
being a constant of proportionality. This is recognizable as an inhomogeneous second-order differential equation with constant coefficients. It is in fact the equation of forced simple harmonic motion.
Exercise:
Show that the solution
s
(
t
) to equation (20.2), satisfying the simplest initial conditions
s
(0) = 0 and
s
′(0) = 0, is given by
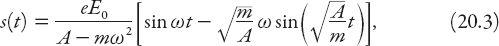
provided that A ≠
mω
2
. In the event that these quantities are equal—a case known as resonance, which will not be pursued here—the solution can be found directly from the original differential equation or by applying L’Hôpital’s rule to the solution (20.3).
Exercise:
Show that the solution for
s
(
t
) when
A
=
mω
2
is given by
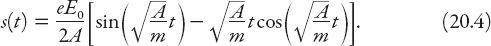
Returning to equation (20.3), we note that, because of the “tight binding” of electrons in most aerosols, the term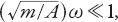 so the second term usually can be neglected. Then the electron
so the second term usually can be neglected. Then the electron
acceleration
can be approximated by the expression

The amplitude of this acceleration is proportional to
ω
2
E
0
. Recall that the electric field (and hence acceleration of the electron) is perpendicular to the direction of the incident wave. Reversing this, we anticipate that the electric field of the scattered wave will be proportional to the
perpendicular
component of the acceleration at large distances from the particle, that is, to
a
sin
θ
z
, where
θ
z
is the angle between the direction of the scattered light and the
z
-axis (see
Figure 20.4
), which is the direction of the incident electric field. We also expect that the total electric field is proportional to the number of electrons present in the particle, and therefore to its volume
V
. The
intensity I
s
of this scattered light is proportional to the square of the electric field, and allowing for the usual inverse square fall-off with distance
r
, consistent with energy conservation, we arrive at the proportionality relation
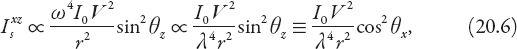
where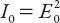 . The scattered wave makes an angle
. The scattered wave makes an angle
θ
x
=
π
/2 −
θ
z
with the forward direction (
x
-axis). We have therefore obtained a fundamental result for Rayleigh scattering, namely that the intensity of scattered light is inversely proportional to the fourth power of the wavelength. More accurately, the probability that a photon of sunlight will be scattered from its original direction by an “air molecule” is ∝
λ
−4
. In any case, a higher proportion of blue light (
λ
≈ 0.4
μ
) than red light (
λ
≈ 0.7
μ
) is scattered, in fact about (7/4)
4
≈ 9 times more.
