X and the City: Modeling Aspects of Urban Life (24 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

A related problem is this: suppose that we are driving along a road in the right-hand lane for which, at the present speed, our stopping distance is
D
.
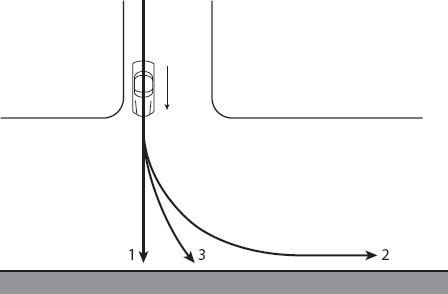
Figure 8.3. The three maneuver options open to the driver.
There is an obstacle ahead—it might be a repair crew, a stalled truck, or even a vehicle moving more slowly than we are (in the latter case we must adjust our speed in the calculations to that relative to the vehicle). What is the maximum obstacle width
W
that can just be avoided by turning left in a circular arc (if traffic in the adjacent lane permits this maneuver)?
We already know that the turning radius is twice the stopping distance. From
Figure 8.4
we see that the angle
β
=
α
/2. Here
β
is the angle subtended by the obstacle and the vehicle before the maneuver begins, and
α
= arcsin (1/2) = 30°, so
β
= 15°. The width of the obstacle at this distance is therefore
D
tan
β
≈ 0.268
D
. A wider obstacle cannot be avoided except by stopping.
Exercise:
From the figure show that tan 15° = 2 −.
Let’s try to estimate some typical stopping distances for a range of speeds. This distance depends on the coefficient of friction (
μ
) between the tires and the road, and the driver’s reaction time. The
minimum
such distance
D
m
can be found by ignoring the latter, as long as one adds the “reaction time × speed” distance
D
r
afterward. The frictional force must reduce the kinetic energy of the car to zero over the distance
D
m
. Provided the wheels do not lock during the deceleration (no sliding or skidding occurs), we use the coefficient of
static
friction. If the wheels are locked, the braking force is due to
sliding
friction, which is in general different, as noted earlier. In the case of static friction, for a car of mass
m
, the equation to be satisfied is therefore
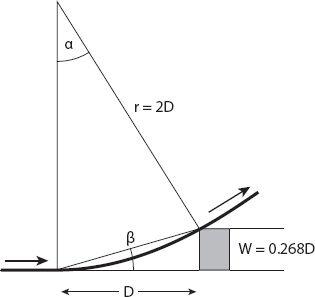
Figure 8.4. Geometry for turning to avoid a slower vehicle.

from which it follows that

Examining this result, we note that it is independent of the mass (or weight) of the car. It is also proportional to the square of the initial speed; thus doubling the speed
quadruples
the minimum stopping distance. The value of the coefficient
μ
depends on the quality of the tires and the prevailing road conditions; probably the best realistic value is
μ
= 0.8, but for more worn tires, or wet roads, a somewhat lower value 0.7 or 0.6 is probably appropriate (or even lower for tires in poor condition). Here are some minimal (rounded) stopping distances for various speeds, taking
μ
= 0.65. Also included, for illustrative purposes, is
D
r
, the distance covered in a nominal (and somewhat slow) reaction time of one second. The fourth column is the approximate total distance (
D
T
) required to stop at these speeds, given the above assumption.

For simplicity we now consider a minimal stopping distance of 100 ft, corresponding to a speed of about 44 mph (71 km/hr). If the vehicle is able to pass the obstacle without braking at all, this maneuver will begin after the reaction time. This means that the vehicle can pass a large obstacle of width nearly 27 feet if traffic in the adjacent lane(s) permits. But then the direction of the car will be at an angle of 30° to the original direction, a dangerous predicament to be sure!
To improve the safety of this maneuver, consider the following modification: we require that once abreast of the obstacle, the car should be moving parallel to the road in the new lane. For this case, the geometry changes a little (see
Figure 8.5
). Now the car’s “trajectory” will be a sigmoidal-type shape composed of two smoothly joined circular arcs as shown. As before
β
=
α
/2, but now
α
= arcsin(1/4) ≈ 14.48°, so
β
≈ 7.24°, meaning that the width of the obstacle should not exceed
D
tan
β
≈ 0.127
D
for the maneuver to be executable. For a value of
D
= 100 ft, this is just less than 13 ft, which allows for a few feet of clearance around a large truck.
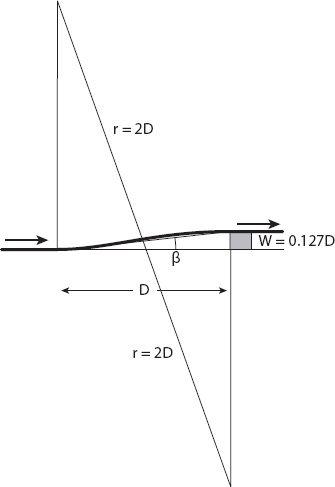
Figure 8.5. Modified geometry for turning to avoid a slower vehicle.
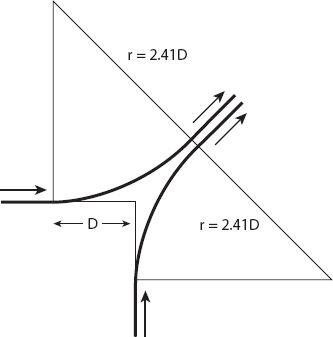
Next we consider two cars approaching an intersection perpendicularly at the same speed, as shown in
Figure 8.6
. Suppose that each driver instinctively tries to swerve to the side by at least 45°; we will take this as a lower bound, for then they end up moving parallel to each other (if road conditions permit, of course). The angles of the truncated triangle are each 45° and therefore by symmetry the line joining each vertex to the corner of the junction makes an angle exactly half this with the hypotenuse. Recall that the minimum distance required for a “straight stop” is
D
and that for a circular arc is 2
D
. Now the radius of the arc shown in
Figure 8.6
is
r
=
D
cot(
π
/8) ≈ 2.41
D
. From equation (8.8) we can compare the corresponding speeds for the circular arc (1) and the 45° swerve (2):
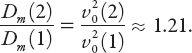
This implies that
v
0
(2)/
v
0
(1) ≈ 1.1, that is, the speed can be about 10% greater in the 45° swerve.