Nonplussed! (47 page)
Authors: Julian Havil

THE BINOMIAL INVERSION FORMULA
Suppose that we have a function
f(r,s)
of two positive integer variables and that we wish to sum its values over the infinite, diagonal half-plane:
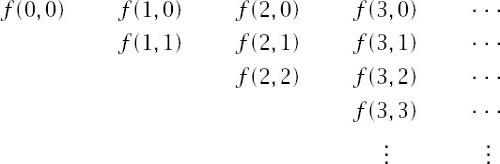
We could add all of the terms together in two obvious ways:
(1) Take each row one at a time and add the terms in it and then add the sums of these rows. The sum of the
s
th row is
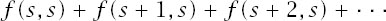
and adding these contributions from each row is achieved by
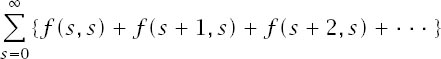
and this sum can be compactly written as the double sum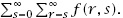
(2) Take each column one at a time and add the terms in it and then add the sums of these columns. The sum of the
r
th column is
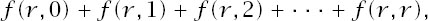
where each sum is finite, ending at the appropriate diagonal element. Adding these contributions from each column is achieved by
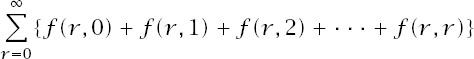
and this sum can be compactly written as the double sum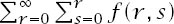
Put these observations together and we have the identity
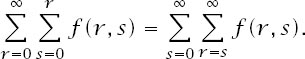
Now for the formula.
If two sets of numbers
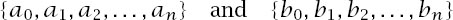
are related by the condition
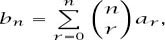
then
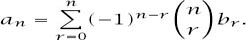
The plan is to define two generating functions
A(x)
and
B(x)
by
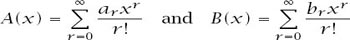
and write
B(x)
in terms of
A(x)
. This will allow us to accomplish the reverse identity of writing
A(x)
in terms of
B(x)
and this in turn will enable {
a
0
,
a
1
,
a
2
,…,
a
n
} to be written in terms of {
b
0
,
b
1
,
b
2
,…,
b
n
}.
Using the definition of the
b
r
and substituting them into the definition of
B(x)
results in