Nonplussed! (40 page)
Authors: Julian Havil
To end with we list, for the frugally minded, the years between 1901 and 2099 in which an old calendar can be reused, under the assumption that the interest is in which dates fall on which days of the week, rather than the irregular holidays such as Easter.
Table 13.8
summarizes the information for year
X
, which is characterized by the number of years
X
is after a leap year.
Notice that the expression
X+
28 occurs in all four rows, which means that a calendar can always be used every 28 years.
Incorporating the requirement that Easter will also be on the same day brings with it considerable serendipity. For example, the calendars for the years 1981 and 1987 are identical, including the date for Easter, whereas the calendar from 1940 will not be reusable until 5280!
FRACTRAN
Everything should be made as simple as possible, but not simpler.
Albert Einstein
Mysterious Arithmetic
In
chapter 6
we looked at one idea from the fertile and original mind of John Conway, and now we will look at a second, which, in typical whimsical style, he called ‘fourteen fantastic fractions’ in his joint publication with Richard Guy,
The Book of Numbers
. The idea appeared earlier, in his article
Fractran: A Simple Universal Programming Language for Arithmetic
, which constituted
chapter 2
of the 1987 book
Open Problems in Communication and Computation
(ed. T. M. Cover and B. Gopinath), Springer, pp. 4–26. Further articles about the construction abound; we have used one of Richard Guy’s from
Mathematics Magazine
: ‘Conway’s prime producing machine’ (1983) 56:26–33.
The fractions in question are the seemingly arbitrarily ordered collection
with each labelled with a letter of the alphabet for easy reference.
We will now play a seemingly arbitrary game with the seemingly arbitrary fractions. Start with the integer 2 and multiply it in turn, starting at A, by each of the fractions until we arrive at a new integer: clearly, it is the fraction M which results in success, yielding 15 as the product. The process is repeated with the new integer (15), again starting at A and continuing to the first fraction to yield an integer product once again (N in this case, yielding 825). This is repeated indefinitely, but each time an exact power of 2 is reached, that power is noted. At this stage it is not at all clear that a power of 2 will be reached at all, let alone more than one of them; in fact, an infinite number of them will be reached, and those powers form a very important sequence of positive integers. With the intrigue thus built up, we will look at the first stages of what results from this opaque process, listing as a pair the current integer and the fraction which yields the first integer product:
and we have reached the first power of 2 after 19 steps; that power is itself 2. The reader can easily check the list with a calculator but to proceed further really needs an appropriate computer program and using one confirms that the next power of 2 to be reached is 8 (after 69 steps) and the one after that is 32 (after 281 steps). For those interested, the full list of generated integers up to this stage is given in
figure 14.1
.
A Mystery revealed
What is so special about the process? If we perform it repeatedly, we arrive at the list of generated powers of 2:
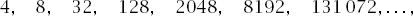
or, written in exponential form, 2
2
,2
3
,2
5
,2
7
,2
11
,2
13
,2
17
,… and the exponents are none other than the prime numbers in order;
in fact, incredible though it may seem, this process is nothing other than a prime-producing procedure: every prime will be generated, in order. Conway called this process PRIMEGAME.
Figure 14.1.
The sequence to reach 32.
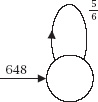
Figure 14.2.
The loop corresponding to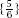
The generation of prime numbers is a perfectly straightforward programming problem and therefore, in principle, a simple computational matter, but why should this arithmetic trick achieve what a programming language naturally succeeds in? The answer is that it really is a programming language in disguise.
To begin an explanation, we will frame the process in a more general context:
(1) Decide on an ordered list of fractions and a starting integer,
N
.
(2) Multiply the current integer (initially
N
) by the first fraction in the list for which the product is itself an integer and so obtain a new integer.
(3) Repeat step 2 until no product produces an integer, in which case the processes stops, or continue it indefinitely.
For example, suppose that our list is populated by a single fraction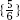
and suppose also that our starting integer is
N
= 648.We can represent this recycling process by the loop as shown in
figure 14.2
and by the more formal pseudo-programming statement:
which we will take to mean ‘multiply the input by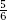
and continue doing so for as long as the input is an integer by starting again at line 1’.
This seemingly random pair of choices of fraction and input causes the loop to be traversed exactly three times before fractions have to be introduced, which brings the process to a halt with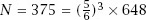
. So what?
