Nonplussed! (46 page)

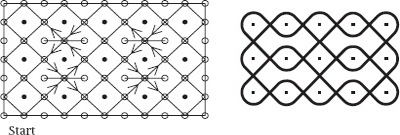
Figure 6.

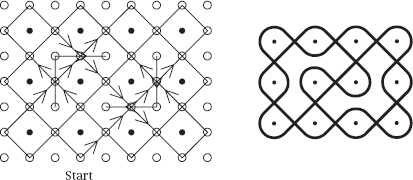
Figure 7.

As another example of the effect consider the 3
×
5 array which appeared at the start of
chapter 10
and which, of course, can be traced in one continuous loop. Its dot pattern, to which has been added four small horizontal, two-way mirrors, is shown on the left of
figure 6
. The resulting smoothed motif is, again, on the right; it and its bigger versions are given the name ‘Lion’s Stomach’.

The 3
×
4 array of
chapter 9
can be enhanced by the inclusion of two sets of two-way mirrors set at right angles to each other, as shown on the left of
figure 7
; again, the smoothed version is shown on the right of the figure. This is the ‘Chased Chicken’ design.

These motifs, then, provide a link between art, African culture and mathematics, with the Euclidean Algorithm making a somewhat surprising appearance. For further exploration of these and other related ideas the reader is referred to the works of Paul Gerdes, starting with
Geometry from Africa: Mathematical and Educational Explorations
, published by The Mathematical Association of America.

THE INCLUSION – EXCLUSION PRINCIPLE

This is used to count the distinct elements in any number of overlapping sets. To begin with, consider the Venn diagram in
figure A.1(a)
, in which just two sets intersect.

To calculate the total number of elements we can add all of those elements in set
A
to all of those in set
B
, but in doing so we have counted those in the intersection twice and so we subtract one count of the elements in the intersection. Put symbolically,

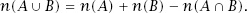
With the three overlaps, as in
figure A.1(b)
, we adopt the same process, this time subtracting all elements in the three intersections, but in doing this we have now eliminated those in the intersection of all three sets. If we add these back in, we arrive at the expression

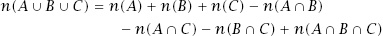
In general,

We can convince ourselves that the process does count every element precisely once by the following argument.

Figure A.1.

Suppose that an element
x
belongs to exactly
r
of the sets. The first step has us count all of the elements in all of the sets, disregarding overlap; this means that
x
is counted exactly
r
times. There are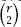
pairs of the sets in which
x
appears, so we need to subtract this number from
r
; then we need to add in the number of times that
x
appears in set triples, which is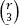
, and continue doing this until we reach
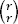, which is 1. Therefore, the process counts
x
precisely

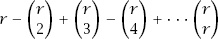
times.

Now notice that the expression

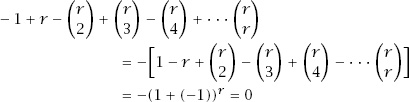
and so

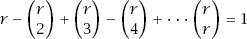
and the process has indeed counted
x
precisely once.