Nonplussed! (44 page)

and we have a machine which moves between states, possibly altering the contents of certain dynamic registers.

Fibonnaci Game

As a final precursor to dealing with PRIMEGAME, we will look at FIBONNACIGAME and so go through the procedure that generates any particular Fibonnaci number.

The Fibonnaci sequence is well known to be defined by the recurrence relation:

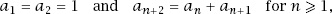
which generates 1,1,2,3,5,8,13,…. To have a computer print out the
n
th Fibonnaci number requires code equivalent to

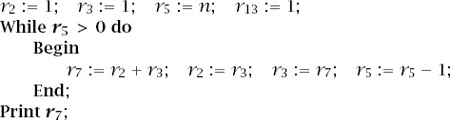
Figure 14.7 represents the process and, with an input of
N =
2 × 3 × 5
ⁿ
× 13, the Fractran-5 program to achieve this is given
below:

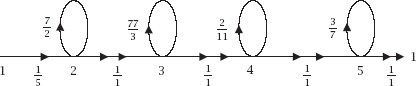
Figure 14.7.
Loops which produce Fibonacci numbers.

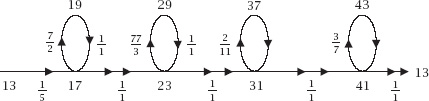
Figure 14.8.
Modified Fibonacci loops.

To convert this to a fraction list we need to eliminate the loops and label the nodes with ‘big’ primes, as in
figure 14.8
, which enables us to write the Fractran-9 program as

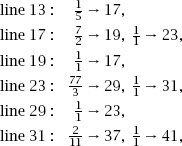
and using Conway’s algorithm to finish with the fraction list

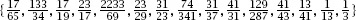
with the final two fractions there to tidy things up so that the process results in the output of precisely 2
^Fib(
n
)
. These final fractions are the equivalent of including one further node, labelled with a 1 and with two loops attached to it. Although the use of a nonprime labelled node and a loop does challenge the constraints of the process, it is fine used in this way, and, in Con-way’s words:

We note that it is permissible to label one of the states with the number 1, rather than a large prime number. The fractions corresponding to transitions from this state should be placed (in their proper order) at the end of the Fractran-1 program. If this is done, loops, provided they have lower priority than any other transition, are permitted at node 1.

He demonstrates the point by amending the fraction list for multiplication to

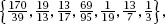
which we leave the reader to ponder!

Finally, to PRIMEGAME.

PRIMEGAME

In factored form its fraction list is

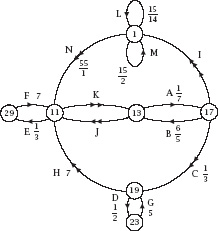
Figure 14.9.
Loops which produce primes.

which can be written as the Fractran-7 program:

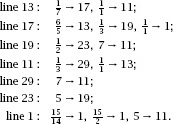
Figure 14.9 represents the process and is altogether more complicated. Its nodes are labelled with the obvious primes and with 1.

At the sixth stage, PRIMEGAME takes
N
= 2 to
N
= 2275, the factorization of which is 5
²
× 7 × 13, at which point
N
is subject to the (AB) cycle. This is a special case of the general
N =
5
ⁿ
× 7
^d
× 13 with
d < n
, which will recur throughout the
process and
figure 14.8
shows what inevitably happens to such a number. It is transformed to a number of the form
N
= 2
ⁿ
× 3
^r
× 7
^d-r-
1
× 17 and then, if
r >
0, it proceeds via the C route to 5
ⁿ
× 7
^d-
1
× 13, whereas, if
r
= 0, it proceeds via the I route to 5
ⁿ⁺¹
× 7
ⁿ
× 13. Now we can interpret this in terms of the integer
n
and its possible divisors
d
by writing
n = q × d + r
in the standard way. PRIMEGAME acting on
N =
5
ⁿ
× 7
^n-
1
× 13, as it does initially with
n =
2, will test all possible divisors of
n
from
n-1
to 1, and then continues with
n
increased by 1. But, if
r =
0, it is the case that
d
divides
n
and therefore
n
will be composite unless
d =
1, in which case
n
will be prime. The number 2
ⁿ
× 7
^d-1
= 2
ⁿ
then provides the only power of 2 that ever arises in the computation, and does so precisely when
n
is prime. Even unveiled, it’s still clever!