Nonplussed! (48 page)
Authors: Julian Havil

Now we invoke the earlier result with
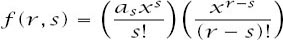
to arrive at
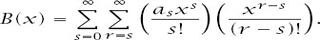
Now we can move the summation over
r
past the expression in
s
to get
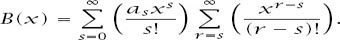
Next we clean up the second summation by writing
t = r -s
and so replacing the variable
r
by the variable
t
to get
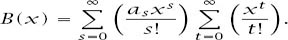
The first summation is
A(x)
and the second simply e
x
, which makes
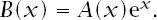
Now we can reverse the identity to get
A(x) =
e
-x
B(x)
and, in turn, this means that
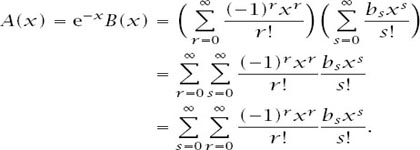
To alter this to a convenient form, replace
r
by
n = r + s
to get

and using the preliminary result once more and introducing
n
! at the top and bottom we have
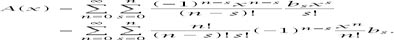
Tidying up and pushing the sigma through results in
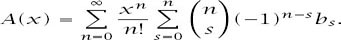
Therefore,
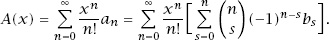
And, equating coe3cients, we finally have the result that
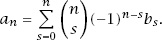
SURFACE AREA AND ARC LENGTH
The element of surface area generated by rotating the elemental piece of curve 360° around the
x
-axis, as shown in
figure C.1
, is given by
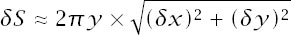
and so
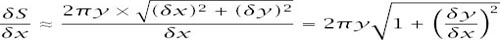
and in the limit
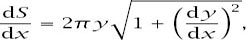
which makes the total surface area
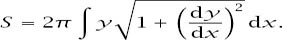
Arc Length of a Curve
Take an arbitrary smooth curve and an origin O, then in the standard calculus notation of
figure C.2
, and using Pythagoras’s Theorem in the upper pseudo-triangular, elemental region we get
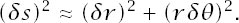
We can choose to divide both sides by
δr
2
to get
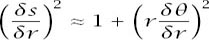
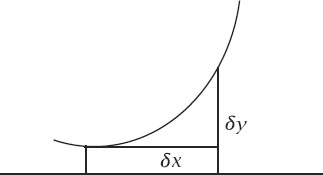
Figure C.1.
Element for surface area.
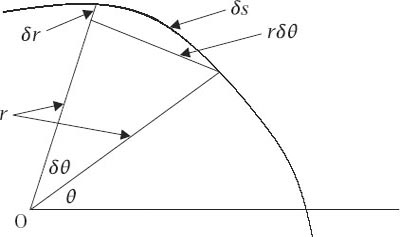
Figure C.2.
Element for arc length.
and in the limit
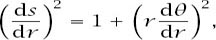
which makes
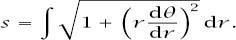
Alternatively, we can choose to divide both sides by
δθ
2
to get

and in the limit
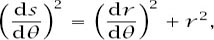
which makes

