Nonplussed! (41 page)
Authors: Julian Havil

In fact,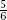 and
and
N =
648 are not at all random choices; it is no small matter that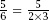 and that
and that
N
= 648 = 2
3
×3
4
is an example of a number which is of the form
N
= 2
n
×3
m
for some nonnegative integers
m
and
n
. The factorization of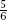 shows that each multiplication by it will decrease the powers of 2 and 3 in the representation of
shows that each multiplication by it will decrease the powers of 2 and 3 in the representation of
N
each by 1 and increase the power of 5 by 1, and this will continue for as long as the product is an integer; that final integer is 375 = 3 × 5
3
.
If we consider the values of the powers of 2, 3 and 5 in the representation of
N
to be values held in the dynamic registers
r
2
,
r
3
and
r
5
, respectively, in the general case we start with
r
2
=
n
,
r
3
=
m
,
r
5
= 0 and finish with either
r
2
= 0 or
r
3
= 0 and
r
5
= min(
m,n
); the contents of the 5 register finishes with the minimum of the two integers
m
and
n
and the process is seen to be precisely one of finding the minimum of two nonnegative integers. In terms of a typical, real programming language this is equivalent to
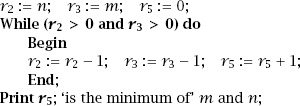
We can see that this simple process is therefore equivalent to a conventional programming algorithm.
Change the fraction to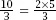 for the same input of
for the same input of
N
= 2
n
×3
m
as in
figure 14.3
and the process adds 1 to each of
r
2
and
r
5
and subtracts 1 from
r
3
, until
r
3
= 0, at which point
r
2
=
m + n
and
r
5
=
m
and the 2 register contains the sum of
m
and
n
; we have an adding machine. This time the equivalent code is
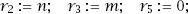
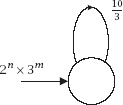
Figure 14.3.
The loop corresponding to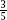
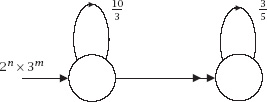
Figure 14.4.
The loop corresponding to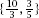
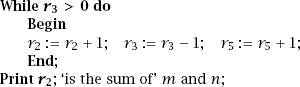
We can tidy up this last solution and at the same time prepare it for generalization by introducing the second fraction of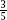 at its end and so form the fraction list
at its end and so form the fraction list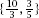 .
.
figure 14.4
represents this, with the agreed convention that single arrow routes have precedence over double arrow routes.
