Nonplussed! (39 page)

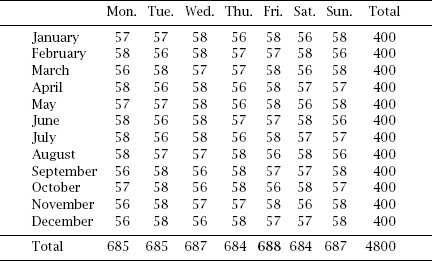
To compile our data, therefore, we simply need to count up the frequencies with which the 13th of the month falls on each day of the week in a cycle of 400 years, and to do this we can program a computer to use Gauss’s day of the week formula; the results of this computer calculation are given in
table 13.3
.

A look at the bottom row reveals that the 13th of the month falls on a Friday 688 times out of the possible 4800, just beating Wednesday and Sunday. Professor Lyttleton is vindicated, as he is with the remainder of his statements.

Table 13.3.
Frequencies with which the 13th of the month falls on each day of the week in a cycle of 400 years.

The Remainder of the Letter

Lyttleton’s final paragraph contains the comforting observation, ‘that the first day of a new century can never fall upon a Friday’. Care must be taken with what he means by the statement; for example, 1 January 2100 will be a Friday. He has taken the view that, since there is no year 0, the first day of the new century will have the year part of 01, for example, 1 January 2101. In fact, more can be said, in that
the first day of a new century can never fall on a Friday, Wednesday or Sunday.

To see this we should agree that, since we are interested in January,
m =
1 and so we must use a year part of 00 for the calculation of
c
and
g
, making
g =
0. The calculation is, then,
w
= (1 + 0 +
f
+ 0 + 0) mod 7 = (1 +
f
) mod 7. If we in turn substitute {0,1,3,5} (the four possible values of
f
), we arrive at the equations

the solutions for which are
w =
1,2,4,6, respectively. This
means that 1 January of a new century can only start on a Mon-day, Tuesday, Thursday or Saturday; omitted from the list is that dreaded Friday and Wednesday and Sunday as well.

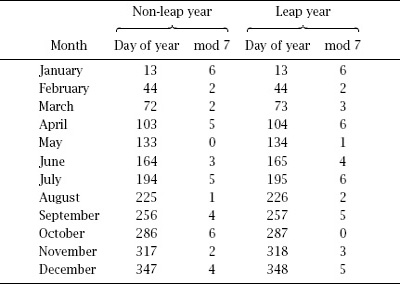
Table 13.4.
When in the year the 13th of the month occurs.

In Lyttleton’s second paragraph, he refers to the frequency with which Friday the 13th occurs in a year and we will look more closely at this aspect of that most unpropitious day.

If we take a non-leap year and number the days from 1 January to 31 December from 1 to 365, we can tabulate which day of the year corresponds to the 13th of each month. For example, 13 January is the 13th day of the year, 13 February is the 44th day of the year, 13 March is the 72nd day of the year, etc. If we reduce these numbers modulo 7, we can ascertain on which day of the week each date of the 13th occurred, provided we know on what day of the week 1 January occurs. The same enumeration can be used for leap years and
table 13.4
summarizes the results.

Now we need to consider the implications for Fridays, given that 1 January falls on each of the days of the week, to arrive at the first two columns of
table 13.5
. Cross-referencing with
table 13.4
results in the third column of
table 13.5
, which lists
the months having Friday the 13th in them.
Table 13.6
again repeats the whole thing for leap years.

Table 13.5.
Restrictions for a non-leap year.

Table 13.6.
Restrictions for a leap year.

From these last two tables we can deduce the following:

• There is at least one Friday the 13th in every year.

• The greatest number of occurrences of Friday the 13th in any year is three. Also, these must occur in February, March and November in a non-leap year and January, April and July in a leap year.

The year 1970 was not a leap year and so the triplet of months had to be as Lyttleton had it. Since every month appears in the right-hand columns of
tables 13.5
and
13.6
, the average number of Friday the 13ths in every year is simply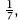
, or 14%; the full
calculation for a non-leap year is

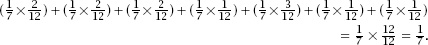
• The only possibility for consecutive months having Friday the 13th in them is February and March and this can only occur in a non-leap year. The next few years are 2009, 2015 and 2026.

The final part of the letter is whimsical, but it does provide the motivation for the second recondite algorithm, one which computes the day on which Easter Sunday falls in any particular year. With Easter Sunday defined as the first Sunday after the first full Moon to occur after the vernal equinox (21 March), it is small surprise that the computation of its date is somewhat complex; it is no surprise at all that Gauss provided an algorithm for this computation too. That said, his procedure is a little inelegant in that there are exceptions to consider, and we choose to present an algorithm which has none such and which seems to have its origins in the early nineteenth century with the French mathematical astronomer and contemporary of Gauss, Jean Baptiste Delambre; it is valid for all Gregorian years, that is, for 1583 and beyond.

The left-hand column of
table 13.7
provides the algorithm and the right-hand column a single check of it. (The months are numbered naturally from January (1) to December (12).)

The calculation tell us that Easter Sunday in 2005 fell on 27 March, and it did! In fact, it can be shown that Easter Sunday can fall on one of 35 dates: 22 March to 25 April.

And what of Ascension Day? This is the 40th day after Easter Sunday and commemorates the Ascension of Christ into heaven, according to Mark 16:19, Luke 24:51 and Acts 1:2. And, to save counting, an alternative name provides a strong hint that it cannot fall on a Friday: Holy Thursday (not to be confused with Maundy Thursday).

And Pancake Day? This is the English term for the day before the beginning of Lent, 47 days before Easter Sunday: no counting
is needed here either; Lent begins on Ash Wednesday, one day after Shrove Tuesday, otherwise called Pancake Day.

Table 13.7.
A test of the Delambre formula.

And what of superstition? Eggs laid on Ascension Day are said never to go bad and will guarantee good luck for a household if
placed in the roof, and in some parts of England the first pancake made on Pancake Day is given to chickens, to ensure their fertility during the year.

Table 13.8.
The reuse of a calendar.