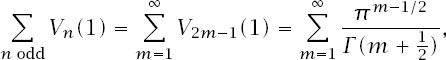Nonplussed! (35 page)

So, a hypersphere of radius 1 achieves its maximum volume in 5.256 946 4 …-dimensional space.

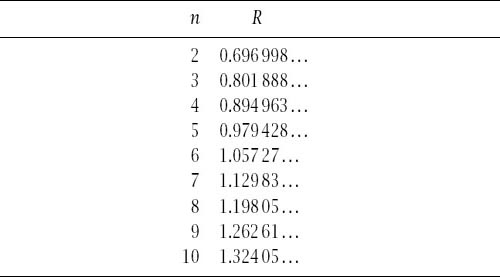
What must the radius of the sphere be to achieve its maximal volume in precisely five-dimensional space, or for that matter what must the radius of the sphere be to achieve its maximal volume in any other integral dimensional space? To answer these questions we need to consider the general
V
_n
(
R
) and differentiate it with respect to
n
just as we have done previously. The almost identical calculations are

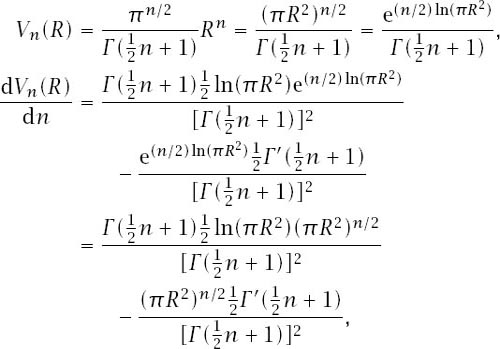
Table 12.2.
Radius for maximal volume.

and d
V
_n
(
R
)/d
n
= 0 requires that

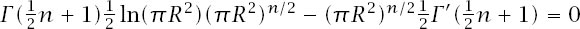
and so

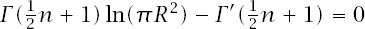
and

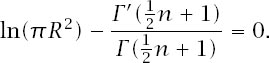
We have the general condition that

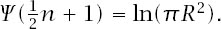
Table 12.2
shows the values of
R
for which a hypersphere of that radius achieves its maximal volume in low integral dimensional space. That is, a hypersphere of radius 0.696 998 … achieves its maximum volume in two dimensions, one of radius 0.801 888 … achieves its maximum volume in three dimensions, etc.

Sums of Volumes

The transcendental Gelfond Constant, e
^π
, appears naturally when we probe a little further into unit hypersphere volumes
and investigate (ignoring units of measurement) the total volume of the infinite sequence of them. Since

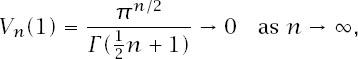
there is at least a chance that there is a value to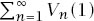
and, if we evaluate the finite sum for a large number of terms, our optimism seems to be well founded with that sum equal to 44.999 326 089 382 855 366 ….

To find a closed form for this we will again need to consider even and odd dimensions separately.

Recall that, for
n
even, we may write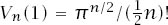
for
n
= 2,4,6,… and, if
n
= 2
m
, we have that
V
_2
m
(1) =
π
^m
/
m
! for
m
= 1,2,3,…. This means that

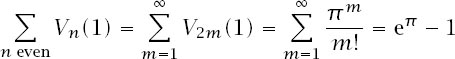
and we have the promised appearance of Gelfond’s constant.

Matters are far more complicated if
n
is odd. Now we have that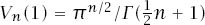
for
n
= 1, 3, 5,… , and, if
n
= 2
m
− 1, we have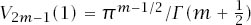
for
m
= 1, 2, 3,… and the sum of the volumes is now