Nonplussed! (38 page)
Authors: Julian Havil

which generates
table 12.4
.
In summary, the unit hypersphere has a maximum volume of 5.277 768 … in 5.256 946 4 …-dimensional space and a maximum surface area of 33.1612 … in 7.256 95 …-dimensional space. Further, a hypersphere of radius 0.696 998 … achieves its maximum volume, and one of radius 0.422 751 … its maximum surface area in two dimensions; one of radius 0.801 888 … achieves its maximum volume, and one of radius 0.574 578 … its maximum surface area in three dimensions, etc.
(Using very similar techniques as before, the sum of the surface areas of hyperspheres can be shown to be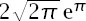 for even dimensions and
for even dimensions and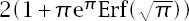 for odd dimensions, making the total
for odd dimensions, making the total
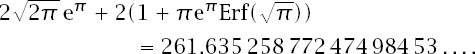
A similar plot to
figure 12.8
again shows that the convergence is all but accomplished by the twentieth term.)
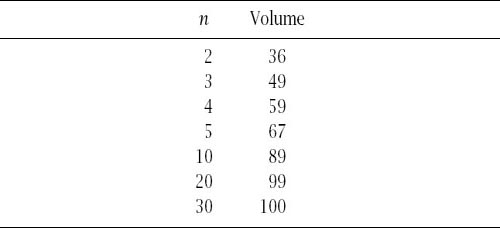
Table 12.5.
Distribution of volume in a hypersphere.
The Distribution of Volume
Is any of this useful? A good answer is, who cares? That said, there are implications of some of the strange behaviour of hyper-space to the theory of sampling in large numbers of variables, and the many mathematical ideas which depend on the techniques. We will not discuss them here but we will show an area which causes problems.
The volume of the
n
-dimensional hypersphere with radius
R
is, of course,
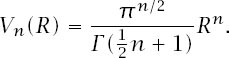
Now we ask the question, Where is this volume? To answer this, we will initially be particular and ask the question, How much of the volume of the hypersphere is at a distance of 20% from its surface?
The answer, as a percentage to the nearest whole number and for varying dimensions, is given in
table 12.5
and the figures clearly show that the volume near the surface is fast approaching 100%.
In general, the amount of volume near the surface of the hyper-sphere of radius
R
can be measured by the difference between the volume of the hypersphere and the volume of the hyper-sphere of radius
R
(1 −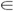 ), where
), where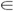 is taken to be small (in
is taken to be small (in
table 12.5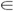 = 0.2). Compare this quantity with the volume of
= 0.2). Compare this quantity with the volume of
the hypersphere itself and we have the fraction
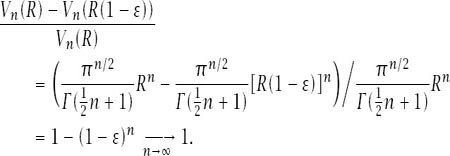
That the asymptotic limit is 1 shows that, whatever volume there is in a high-dimensional hypersphere (and there isn’t much), it is ever more concentrated at its surface. Also, since, for all
R
,
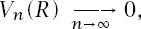
inscribe the hypersphere in the
n
-dimensional hypercube of side 2
R
and we see that most of the hypercube’s volume is concentrated at its corners.
Our discussion has concentrated on a few particular areas of the counterintuitive nature of hyperdimensions and we could mention many other manifestations and implications: the full story is big enough to fill books (and has done so). To pursue the matter further in one important direction, the reader is encouraged to research the term ‘the
curse of dimensionality
’, which was coined by the American mathematician Richard Bellman in 1961.

FRIDAY THE 13TH
I’m a great believer in luck and I find the harder I work, the more I have of it.
Thomas Jefferson
A Letter to the
Times
The bottom right-hand slot of the letters page of the London
Times
is often reserved for offbeat or amusing correspondence and was occupied on Friday, 13 February 1970, by the following:
Sir,
If, as some of your recent correspondents suggest, eccentricity is one of the criteria for publication of letters to the
Times
, you may be willing to allow me, on this doubly unlucky date of Friday the Thirteenth of February, to remind any superstitious among your readers that the 13th day of the month falls more frequently on a Friday than upon any other day of the week.
This at first sight unbelievable property of the calendar as set up is exemplified by the present year, when no fewer than three of the 13th days of the month fall on a Friday; namely in February, March and November – 25 per cent; whereas the average figure would be only 14 per cent.
In case this excess causes alarm and despondency, it may be some consolation that the balance is slightly redressed by the fact that the first day of a new century can never fall upon a Friday. And incidentally, but for different reasons, neither can Ascension Day nor Pancake Day!
Yours truly,
Raymond A. Lyttleton, St. John’s College, Cambridge.
This chapter is a study of the letter and matters related to it.
Superstition
Concern about, or even fear of, the number 13 has been given the seemingly unpronounceable name
triskaidekaphobia
, a Greek compound made from the following parts:
tris
, ‘three’;
kai
, ‘and’;
deka
, ‘ten’ (which makes thirteen); plus
phobia
, ‘fear’. It appears to date from 1911, when it appeared in I. H. Coriat’s
Abnormal Psychology
.
There is any number of justifications for 13 being unlucky: there were 13 present at the Last Supper, in Norse mythology there were 13 present at a banquet in Valhalla when Balder (son of Odin) was slain, which led to the downfall of the gods; Hesiod wrote in
Works and Days
that the thirteenth day is unlucky for sowing, but favourable for planting. What is assuredly not apoc-ryphal is the near-catastrophic explosion on the Moon rocket
Apollo 13
, which occurred later in the same year as Lyttleton’s letter, on 13 April 1970 (a Monday), two days after its launch from the Kennedy Space Center at 14:13:00 EST (13:13:00 CST) from launch pad 39 (3
×
13
)
.
Naturally, to balance matters we have triskaidekamania, which is an excessive enthusiasm for the number 13. And, to shift the
blame elsewhere, tetraphobia, a fear of the number 4, which is most common in East Asian countries (since the pronunciation of the number is close to that of a word for death).
Yet matters are worse, since the letter also refers to Friday and so touches on the condition of paraskevidekatriaphobia, or fear of Friday the 13th. Again, the word is made more natural by examining its Greek root,
paraskevi
, ‘Friday’, and
dekatria
, ‘thirteen’, with, of course,
phobia
at the end.
The origins of Friday superstitions are many: Eve tempted Adam to eat the forbidden fruit, the Great Flood occurred, the start of the linguistic confusion at the Tower of Babel, the destruction of Solomon’s Temple and the death of Jesus Christ all, by tradition, took place on a Friday.
There is a story that, in the eighteenth century, the British government tried to relieve its fiercely superstitious sailors of their fear of sailing on Fridays by building a ship called the HMS
Friday
. However, when she set sail one Friday morning on the 13th, under Captain Jim Friday’s command, she was never seen again.
Whatever the probity of the reasons, our Western civilization is stuck with the belief that both Friday and the number 13 are unlucky and in combination doubly so; such a hold does this belief have that skyscrapers are commonly known to have floor numbering that goes from 12 to 14, and ships still delay sailing to avoid Fridays. Franklin Delano Roosevelt is said to have suffered from triskaidekaphobia but, judging from the final line of Samuel Pepys’s diary entry for Friday, 13 July 1660, he eschewed triskaidekaphobia and indeed paraskevidekatriaphobia:
To bed with the greatest quiet of mind that I have had a great while.
Now we will look at the reason that
the 13th day of the month falls more frequently on a Friday than upon any other day of the week.
The mathematics involved is contained in two of the more strange of the elementary formulae to come from the minds of mathematicians, the first from the greatest mind of them all.
Table 13.1.
Values of
e
for each month
m
.

Table 13.2.
Values of
f
for each century
c
.
Gauss’s Formula
This opaque formula is one of several that have been developed to establish the day of the week of a given date and, for the reader who would like to see exactly where it comes from, it has been analysed, in particular, by Berndt Schwerdtfeger (in his Internet article
Gauss calandar formula for the day of the week
1
): we will simply state it and put it to use, but to state the formula we need to establish some notation.
The variable
w
enumerates the day of the week, with
w =
1 corresponding to Monday,
w =
2 corresponding to Tuesday, etc. The variable
d
is the day of the month, so
d {1,2,3,…,31}. The variable
{1,2,3,…,31}. The variable
m
is the number of the month, beginning with January and finishing in December, so
m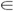 {1,2,3,…,12}. The variable
{1,2,3,…,12}. The variable
y
is the year, given as a four-digit integer,
c = |y/
100| is the two-digit century and
g = y -
100
c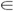 {0,1,2,…,99} is the two-digit year of the century.
{0,1,2,…,99} is the two-digit year of the century.
The month
m
has associated with it a variable
e
, the values of which are given in
table 13.1
. The century
c
has associated with it a variable
f
, the values of which are given in
table 13.2
.
Lastly, there is one more rule: if
m =
1 or 2, then
y
is replaced by
y
−1 in the calculations of
c
and
g
.
With all of this mathematical alchemy in place, Gauss’s formula for the day of the week of any date in the Gregorian calendar is
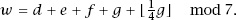
In all of this, [
x
] is the floor function, defined as the greatest integer less than or equal to
x
, as we have seen earlier in the book.
The Big Count
To establish the fact that the 13th of the month is more likely to fall on a Friday than on any other day of the week, we need to look carefully at the implications of the adoption of the Gregorian calendar. The calendar is named after Pope Gregory XIII, who instituted it in 1582 when he decreed that the day after 4 October 1582 would be 15 October 1582 (to considerable public consternation). It is a modified version of the Julian calendar, named after Julius Caesar, and which, by that time, was badly out of synchronization. In the Gregorian calendar the leap year that occurs once every four years is omitted in years divisible by 100 but not divisible by 400. This means that, for example, 2000 was a leap year (since it is divisible by 400) but 2100 will not be (since the number is divisible by 100 but not 400). This carries the important consequence that the Gregorian calendar repeats itself precisely every 400 years, since the number of days in 400 Gregorian years is 100(3 × 365 + 366)−3 = 146097 and this is an exact number of weeks, since 146 097 is exactly divisible by 7.
