Nonplussed! (34 page)
Authors: Julian Havil

and using the substitution
t
=
u
2
, we have that d
t
/d
u
= 2
u
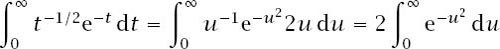
and and this means that
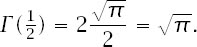
It is then the case that for
n
even
V
n
(1) can be rewritten yet again, this time as
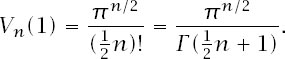
The really nice thing is that this notation unifies the two formulae and it is easy to check that the Gamma function form of the formula holds whatever the parity of
n
.
For example,
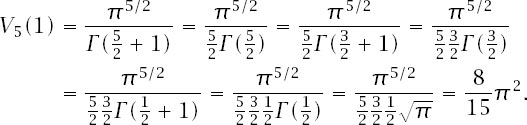
Figure 12.6
is the plot of the continuous form of
figure 12.5
, this time for
n
up to 20. It shows a little more clearly that the maximum occurs a little to the right of
n
= 5 and calculus should help us to find the coordinates of that point, provided that we can differentiate the components of
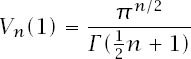
with respect to the continuous variable
n
.
The top of the fraction is easy to deal with using the fact that
a
b
= e
b
ln
a
so that the formula becomes
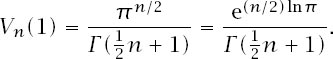
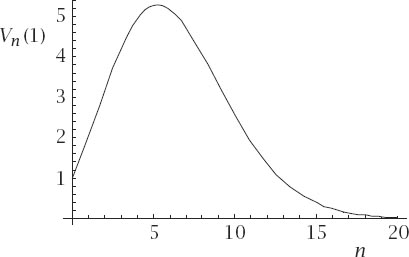
Figure 12.6.
Volume of the unit hypersphere compared with continuous dimensions.
The bottom of the fraction requires us to differentiate the Gamma function. We have no need to look closely at the implications of this and we will merely write the derivative in the usual way as
Γ
′(
x
); what we will need is the even more exotic Digamma function
Ψ
(
x
), which is defined by
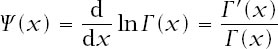
and some powerful mathematical software to evaluate it.
Using the standard chain and quotient rules, the calculations are
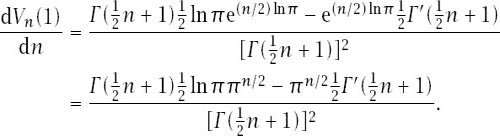
The requirement that d
V
n
(1)/d
n
= 0 means that
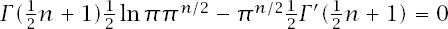
and so
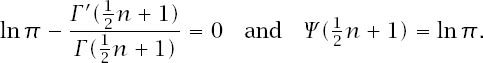
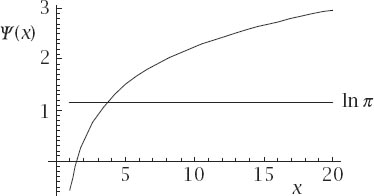
Figure 12.7.
The Digamma function
Figure 12.7
shows a plot of the Digamma function and the horizontal line at ln
π
. To find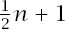 and hence
and hence
n
we need computational help to establish that
n
= 5.256 946 4 … and so is the dimension in which the unit hypersphere has a maximum volume and, substituting this value back into the formula, gives that maximum volume as 5.277 768 ….
