X and the City: Modeling Aspects of Urban Life (58 page)

So: when light is deflected in some manner from its direction of travel, it is said to be scattered. There are several mechanisms that contribute to the scattering of light by particles in the atmosphere: reflection, refraction, and diffraction being the most common, though they are not necessarily mutually exclusive effects. The size of the particles determines which mechanism is the predominant one.

Visibility is reduced to some extent by the absorption of light, but scattering by particles and droplets is the primary source of this reduction. We perceive distant objects by contrast with their environment, and this contrast is reduced by the scattering of light from particles and droplets in the line of sight. Thus visibility is reduced. Depending on their size, particles may settle out of the air in due course; this sedimentation process had already been mentioned in the previous chapter.

Although the particles will be irregular in shape, we can define an effective radius as the average of that of (i) the largest sphere that can be inscribed in the particle and (ii) the smallest sphere that contains the particle. If this radius exceeds about 10 microns (10
⁻⁵
m), they settle out in several hours. As we saw, when an object falls in air, it is subject to at least two separate forces; its weight (acting downward) and air resistance or drag (acting upward). A third force is that of buoyancy (also acting upward), but since the air density is negligible compared with that of the particle, this can be neglected. The particle weight is proportional to its mass and hence to the cube of its radius. As we saw in
the previous chapter, the air resistance is only proportional to its radius, so the weight dominates the drag by a factor that increases as the square of the radius; hence larger particles fall faster, at least initially. As the speed increases, so does the air resistance. If the particle falls from a sufficient height, these competing forces eventually balance each other, and the net force is zero. At this point the particle falls with a constant speed, the terminal speed. On the other hand, if the particles are smaller than 10 microns in size, they can remain suspended in the air for several days, buffeted by air currents.

This, then, is a qualitative summary of the hydrodynamic aspects of sedimentation discussed earlier. By contrast, the optical aspects are more complicated because of the range of particle sizes compared with the wavelengths of visible light (approximately 0.4–0.7
μ
) A convenient measure of relative size is the radius-to-wavelength ratio
R
/
λ
. When this ratio is at least about ten, the particles are considered to be large, and it is convenient to regard light in terms of rays. This is the domain of
geometrical optics
, and as illustrated in
Figure 20.1
, the three processes mentioned above can occur. Light rays can be partially reflected from the surface of the particles, refracted on passing through the interior, or diffracted (“bent”) around the edges. All three mechanisms are exhibited in the phenomenon of the rainbow (see
Appendix 11
); light is refracted and reflected by raindrops to produce this beautiful colored arc in the sky. Less familiar is the third important mechanism—diffraction—a consequence of the wavelike properties of light. This is responsible for some of the more subtle rainbow features—pale fringes below the top of the bow and, as already noted, iridescence in clouds near the sun.

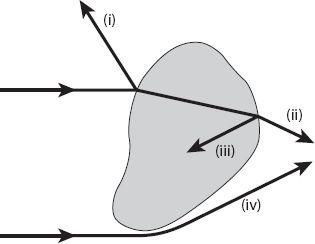
Figure 20.1. Light incident on a large particle may undergo some or all of the indicated processes: (i) reflection at the surface; (ii) refraction into and out of the particle; (iii) internal reflection; and (iv) edge diffraction. Redrawn from Williamson (1973).

For large particles, the amount of light “scattered” by diffraction is as much as that by the other two mechanisms. Some of the refracted light may be absorbed by the particles; if so, this will affect the color of the outgoing radiation. An extreme example of this is black smoke—in this case most of the incident radiation is absorbed. When little or no absorption occurs, large particles scatter light pretty much in the forward direction, so the observer looking toward the light source—the sun, usually—will see a general whitish color. When the particles are not large, the “light ray” approach of geometrical optics is inadequate to describe the scattering processes; the wave nature of light, as mentioned above, must be taken into account. Particles for which
R
/
λ
≈ 1 scatter light in a wider “band” away from the incident direction (resulting in the sky appearing hazy), but smaller particles (for which
R
/
λ
1) are better able to scatter light multidirectionally. If the aerosols are smaller than about 0.1
μ
, the light is scattered much more uniformly in all directions; as much backward as forward and not much less off to the sides. Furthermore, the amount of scattering is very sensitive to the wavelength of the incident light; as we will see below the degree of scattering is ∝
λ
⁻⁴
. This means that the light of shorter wavelength, such as blue or violet, is scattered much more than the longer wavelength red light. Only when we look in the direction of the setting sun, for example, do we see the red light predominating—most of the blue has been scattered out of the line of sight. Think for a moment of cigarette smoke curling upward from an ashtray; typically it is bluish in color—a consequence of the smoke particles being smaller than the wavelengths of light. It is the blue light that is scattered more, and this is what we see.
*
This is an example of
Rayleigh scattering
, the same phenomenon that makes the sky blue. Rayleigh scattering arises because of wavelength-dependent molecular scattering

To understand the phenomenon of scattering from a more analytic point of view, we need to recall some basic physics. An electromagnetic wave has, not surprisingly, both an electric and a magnetic field that are functions of time and space as it propagates. The direction of propagation and the directions of these fields form a mutually orthogonal triad (
Figure 20.2
). And when an electromagnetic field encounters an electron bound to a molecule, the electron is
accelerated by the electric field of the wave. It’s a type of “chicken and egg” situation, because an accelerated electron will also radiate electromagnetic energy in the form of waves in all directions (to some extent), and this is the scattered radiation that we have been discussing. Consider
Figure 20.3
, which illustrates such a situation for a small particle with
R/λ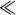
1 as a snapshot in time.

Figure 20.2. Orthogonal triad formed by the direction of the electric and magnetic fields and the direction of propagation for an electromagnetic wave.

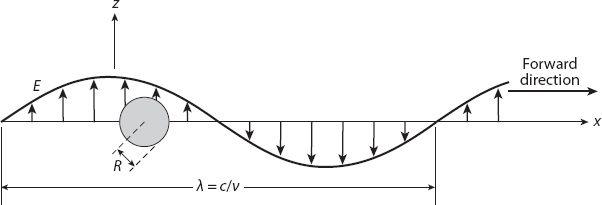
Figure 20.3. A spherical particle of radius
R
λ
experiences a nearly constant electric field
E
. (The wavelength of the incident light is
λ
.) Redrawn from Williamson (1973).

As shown in the figures, the wave propagates with speed
c
in the
x
-direction, with the electric field in the
z
-direction (it is said to be
polarized
in that direction; this is a qualification we shall address below). This field varies periodically with frequency,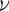
=
c
/
λ
(where
λ
is the wavelength), and its fluctuations affect the electrons it encounters. To a much lesser extent, the more massive nuclei
are also affected, but this will be ignored here. We shall denote the incident electric field by