Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam
X and the City: Modeling Aspects of Urban Life (77 page)

where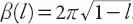 . The approximation (A2.6) for
. The approximation (A2.6) for
A
(
l
) is illustrated in
Figure A2.5
.
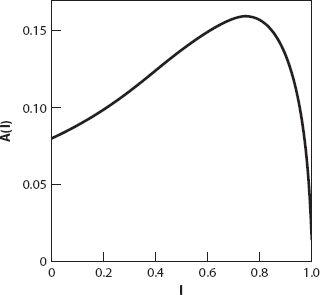
Figure A2.5. The approximation for
A(l)
.
How does this compare with the exact results? The maximum value of
A
(
l
) according to equation (A2.6), occurs when
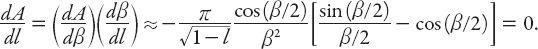
The only value of interest to us is when
β
=
π
, which corresponds to
A
≈ 0.159,
θ
=
π
/2 and
l
= 0.75. Therefore we see that the approximation is “spot on” for the maximum area and where it occurs, but it overestimates the corresponding value of
l
by about 17%.
Comment:
The definition (A2.3) is sometimes called the unnormalized sinc function. The
normalized
sinc function is defined as
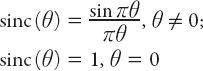
because it may be shown that
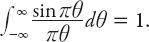
TAXICAB GEOMETRY
If, in New York, you arrive late for an appointment, say, “I took a taxi.”
—Andre Maurois
Imagine a city laid out on a standard rectangular (Cartesian) grid, with blocks defined by equally spaced N-S and E-W roads (of course any directions will do as long as they are perpendicular). Thus to move from location
P
to location
Q
we must travel along these roads; we cannot generally move in a direct line from
P
to
Q
unless we happen to be a pigeon! Let’s compare some of the properties of this somewhat “constraining” geometry with the standard Euclidean one available for the pigeons. Find some graph paper and let’s get started!
Suppose for example that
P
is the point (1, 3), my office, and
Q
is the point (−2, −1), where Starbucks is located. We are of course assuming that the size of each business is small compared with a block distance, so that we can represent them by points. The Euclidean distance between them,
d
E
(
PQ
) is readily computed from the distance formula:
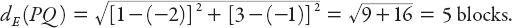
(From now on we will drop the unit of distance “blocks”: it will be understood.) But of course, to arrive at Starbucks from my office I must travel either from
P
to
A
(−2, 3) and then to
Q
, or from
P
to
B
(1, −1) and then to
Q
. In each case the “taxicab” distance is given by
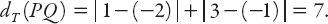
Clearly,
d
T
(
PQ
) >
d
E
(
PQ
) in this case. But inequalities between distances in one geometry are not necessarily preserved in the other. Consider, for example,
the Euclidean distances between (i) the points
R
(1,1) and
S
(3,3), and (ii)
R
(1,1) and
T
(−2, 1), which are, respectively,
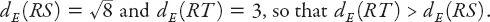
However,
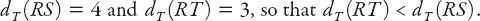
This non-Euclidean geometry, informally known as
taxicab geometry
(see [
44
]) is a form of geometry in which the usual measure of distance in Euclidean geometry is replaced by a new one in which the distance between two points is the sum of the (absolute) differences of their coordinates. This new measure of distance (or “metric”) is also sometimes known as the
Manhattan distance
; in the plane, the Manhattan distance between the point
P
1
with coordinates (
x
1
,
y
1
) and the point
P
2
at (
x
2
,
y
2
) is |
x
1
−
x
2
| + |
y
1
−
y
2
|. Taxicab geometry satisfies all Euclid’s axioms except for the side-angle-side axiom, because one can generate two triangles with two sides of the same length in this metric, and with the angle between them the same and yet they are
not
congruent. For more information on the sometimes surprising properties of this “urban geometry’, consult the delightful little book on this topic by Krause (1986).
Question:
Is Pi equal to four?
Well, as they say, it all depends. . . . If we sketch the set of all points that are a unit Euclidean distance from a fixed point (the coordinate origin, without loss of generality), then we have the unit circle. If we do the same thing but in the taxicab “metric” as it is called, what shape do we get? A little thought, coupled with a sketch or two, reveals that we get a “diamond” shape, that is, a square with two vertices lying on the “
y
” axis and the other two on the “
x
” axis. This is a
taxicab circle
of unit radius! Now we are familiar with the definition of
π
as the circumference of a circle divided by its diameter. With the taxicab metric, the “length” of one side of our taxicab circle is two units, hence the circumference is eight units, and the diameter is two units, so, yes, the taxicab value of “taxicab
π
” is indeed four!

