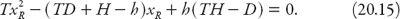X and the City: Modeling Aspects of Urban Life (62 page)

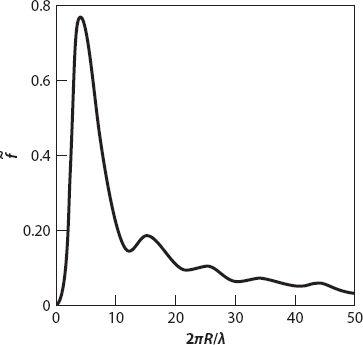
Figure 20.8. Dependence of the relative scattering coefficient
on the ratio 2
πR
/
λ
for a spherical particle with refractive index ≈4/3. Redrawn from Williamson (1973).

We are familiar with rainbows and, perhaps to a lesser extent, with atmospheric halos formed during the day when (very nearly) parallel light from the sun is “scattered” into the observer’s eye by raindrops and ice crystals, respectively. The drops or crystals producing the phenomena are located on the surface of an apparent cone; in the case of the rainbow the axis extends from the observer’s eye toward the so-called anti-solar point (i.e., extending to the shadow of the observer’s head and beyond) as shown in
Figure 20.9
. In the case of, say, the common 22° ice crystal halo (
Figure 20.10
), the axis of the cone extends in a direction from the observer’s eye to the sun.

The reader is encouraged to consult
Appendix 11
if he or she needs to brush up on the basic mathematics behind the formation of these beautiful images.

But have you ever noticed a rainbow-like reflection
from a road sign
when you walk or drive by it during the day? Tiny, highly reflective spheres are used in road signs, sometimes mixed in paint, or sometimes sprayed on the sign. And sometimes, after a new sign has been erected, quantities of such “microspheres” can be found on the road [
37
] near the sign. It is possible to get samples of these tiny spheres directly from the manufacturers, and reproduce some of the reflective phenomena associated with them. In particular, for glass spheres with refractive index
n
≈ 1.51 scattered uniformly over a dark matte plane surface, a small bright penlight provides the opportunity to see a beautiful near-circular bow with angular radius about 22°! (Don’t confuse this with the 22° ice crystal halo; again, see
Appendix 11
.) This bow appears to be suspended above the plane as a result of the stereoscopic effects we now proceed to examine.

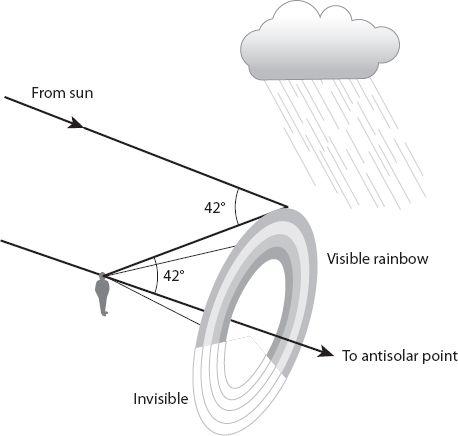
Figure 20.9. Formation of a (primary) rainbow.

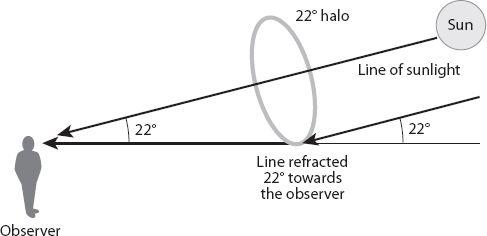
Figure 20.10. Formation of the common 22° ice crystal halo.

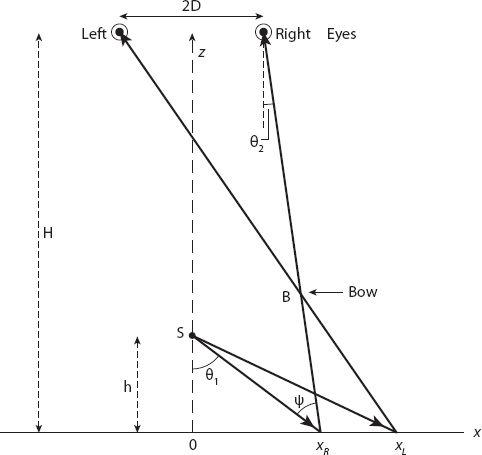
Figure 20.11. Geometry for the “microsphere” bow.

In
Figure 20.11
, representing the
x-z
plane, the (point) source of light is at the point S(0, 0,
h
) and the observer’s right (
R
) and left (
L
) eyes, aligned along the
x
-axis, are located at (±
D
, 0,
H
), respectively, where
H
>
h
. The intersection of the bow with this plane is at the point
B
(
x
_B
, 0,
z
_B
). The ray path
Sx
_R
R
corresponds to a deviation of
δ
= 180° − (
θ
₁
−
θ
₂
) from the original direction. It is an interesting exercise to show that for a sphere of refractive index
n
this deviation is

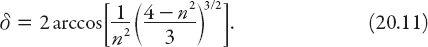
For
n
≈ 1.51.
δ
≈ 2.76 radians, or approximately 158°.

Exercise:
Use equations (A11.3) and (A.11.4) in
Appendix 11
to establish the result in equation (20.11). (The angle
δ
here is
D
(
i
_c
) in equation (A11.4).)

We shall work with the angle
ψ
=
θ
₁
−
θ
₂
≈ 22° in what follows. From
Figure 20.8
we note that

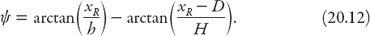
Similarly, for the left eye,

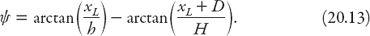
After some rearrangement it follows that

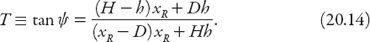
The resulting quadratic equation for the location of
x
_R
is