X and the City: Modeling Aspects of Urban Life (66 page)

Figure 21.9b. Scratches in a stainless steel bowl exhibit circular and elliptical patterns similar to the “rain circle” phenomenon in
Figure 21.9a
. In this picture reflections from two kitchen lights produce the effect.

A very similar phenomenon occurs when you look at the sun through a train or airplane window. The many fine scratches give rise to a similar effect, and for very similar reasons; we only notice those scratches that are perpendicular to the plane of incidence of the light rays. As an example of the same type of thing arising in “kitchen optics,”
Figure 21.9b
shows a similar “rain circle” effect from scratches in a stainless steel mixing bowl. The “circles” are really more elliptical in shape because of the curvature of the bowl.

On a rainy night, light from street lamps reflected by power lines and other cables may be noticed by the observant pedestrian. Let’s assume that you are that person. In
Figure 21.10
, what is the relationship between your position (at
O
say), that of the light and that of the reflection
P
, if any? Since any three noncollinear points define a plane (if we are permitted to assume that your eyes, the light, and its reflection are points here!), and you see the reflection, it follows that
P
lies on an ellipse, with you and the light source as foci. Why is this so? One fundamental property of an ellipse is that the lines joining the foci to any point on the ellipse make equal angles with the tangent line at that point (see
Figures 21.11a
and
21.11b
), and hence with the normal line at that point. This is the law of reflection expressed as a property of the ellipse.

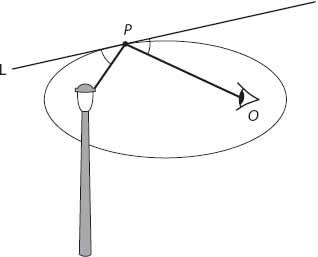
Figure 21.10. The reflection
P
of the lamp in a power line; the lamp and observer”s eye at
O
are at the foci of the ellipse.

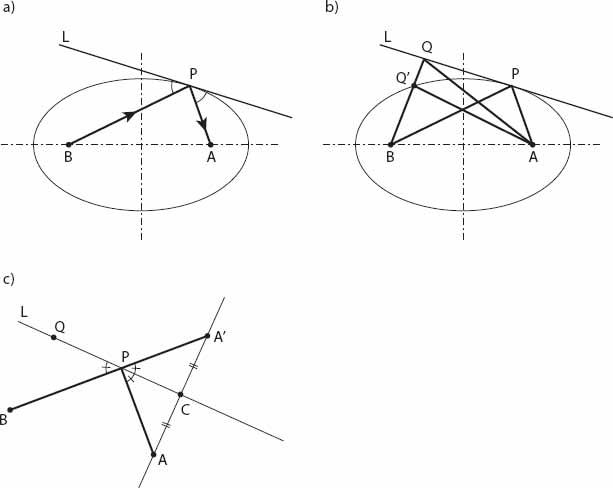
Figure 21.11. (a) Basic geometry of the ellipse with foci
A
,
B
-, and point
P
lying on it, and tangent line at
P
. (b) Construction for the proof;
Q
′ lies on the ellipse. (c) Completion of the proof.

This is proved geometrically as follows.
P
is a point on the ellipse, with tangent line
L
, along which the point
Q
can move. When
Q
is coincident with
P
, the distance
AQ + BQ
is a minimum by virtue of the property that
AQ
′ +
Q
′
B
= constant. Now let
A
′ be the reflection of the point
A
in the line
L
, so that
AC
=
CA
′. Then
AQ
+
QB
=
A
′
Q
+
QB
which is a minimum when
Q
=
P
, and
BPA
is a straight line. This being the case, angles
APC
and
CPA
’ are equal, and hence so are the angles
APC
and
QPB
. The reflective property of the ellipse is established.

Exercise:
Prove this result algebraically (you’ll also need a modicum of calculus).

In a city at night, owing to artificial light sources, we may witness substantial modifications to light pillars, ice crystal halos, and rainbows when the weather conditions are right for producing them. The sources of light are much nearer than the sun (or moon) and thus the light from them is divergent, not parallel. This can give rise to some quite amazing three dimensional “surfaces” that differ significantly from their daytime (parallel light) counterparts. In order to appreciate this, some geometry associated with surfaces of revolution will be required. But before getting into that, let’s ask a much more basic question as an appetizer to the main course, a question that is surely on the minds of everyone in these dark times:

Question:
How many light bulbs are there in Times Square? [
6
]

This is a question that has been radically changed by technology because there are so many types of “light bulbs.” Most of the illumination in Times Square comes from giant electronic billboards rather than from traditional light bulbs. These billboards emit their own light. In fact, each pixel of these billboards does so and could be counted as a separate “light bulb.” To answer the question, then, let’s estimate the number of these pixels. Each electronic billboard has about the resolution of a computer monitor or about 1000 × 1000 pixels = 1 million pixels. There are definitely more than one and fewer than 1000 billboards, so again, let’s use the geometric mean of 30. This gives about 30 million separate illuminated pixels.

Looking at a picture of Times Square, one can’t see that many traditional light bulbs. There are a few scrolling message signs on marquees. They are about 1 letter tall and 50 or so letters long. Each letter will have at least 6 × 8 ≈ 50 light bulbs, so let’s round up to 100. This gives 5000 light bulbs per scrolling message. There are five or ten of those, so that gives another 40,000 light bulbs. The static illuminated signs (traditional neon lights or plastic signs back-lit by fluorescent bulbs) will probably add another few thousand, but that’s just a rounding error.

Now
we can start thinking about the effects of light on ice crystals in the night air—brrr!

As plate-like ice crystals fall they can reflect and refract light. In the daytime
sun pillars
are produced by reflection from the faces of tilted crystals in the vicinity of the rising or setting sun. Specifically, the more common upper pillars result from the reflection of sunlight downward from the lower faces of such crystals, and lower pillars arise from sunlight being reflected upward from the upper faces of tilted crystals. Upper pillars can become brighter as the sun descends below the horizon, and can appear to extend very high up in the sky if the upper crystals have larger tilts than the lower ones (see Adam 2011 and references therein). Artificial sources of light can also produce light pillars as shown in
Figure 22.1
. The angular extent of the pillar is the maximum range of angles (
α
) subtended at the observer’s eye by light reflected from the crystals. This is determined by their distribution in the air between the observer and the light source (though some beyond the source may also contribute). The angular width of the pillar is similarly defined.

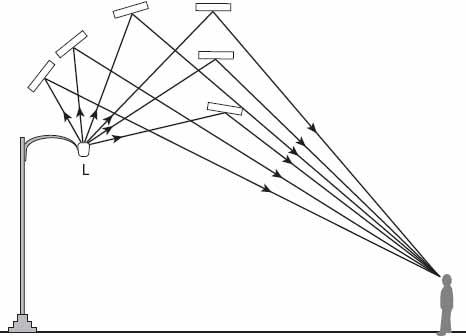
Figure 22.1. How light pillars are formed from ice crystals in the vicinity of a lamp. Each “ray” entering the observer’s eye makes a different angle α with the horizontal direction.

And
now
for some of the more esoteric artificial light phenomena, as promised earlier.

Question:
What is a cone during the day and a cigar or an apple at night?

Answer:
The locus of directions along which one sees an ice crystal halo or a rainbow.

Let’s unwrap this conundrum a little bit. When you look at a small portion of a rainbow, you are looking in a particular direction. Sunlight is scattered by raindrops from this direction into your eyes. For the primary (brighter) bow this direction is at about 42 degrees from the imaginary line joining the sun to the shadow of your head (the antisolar point). Scattered sunlight coming from all other directions at 42 degrees to this line will also reach your eye, resulting in the familiar circular arc we see as a rainbow. Thus we are looking along the
surface of a cone
with half-angle approximately 42 degrees. The same principle
applies to the smaller 22-degree ice crystal halo commonly seen around the sun, or the moon at night; again, we are looking along the surface of a (smaller) cone when we observe this halo. We can think of the rainbow and halo arcs in another way: as the intersection of the imaginary cone with an imaginary plane perpendicular to its axis. And no matter how near or far away the raindrops or ice crystals may be, they give rise to the same circular arcs, because we are looking in
certain directions
; furthermore, rainbows and halos are not
objects
, they are images! Put another way, you cannot “back up” to get more of a rainbow in your camera viewfinder. Of course, if you change your lens for a wide angle one, you can achieve that result! Note that the rainbow, an arc of a circle of angular radius 42° around the antisolar point, is the same as a circle of 138° around the sun. Thus a cone with ‘half-angle’ 138° opens up to the opposite direction; this establishes the notion that bows and halos are intimately connected in a geometrical sense as well as an optical one. This will be a valuable unifying concept in the next section.