Why Beauty is Truth (57 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

In 1984 Michael Green and I did a calculation for one of these superstring theories to see whether, in fact, this anomaly occurred or not. What we discovered was quite surprising to us. We found that, in general, there was indeed an anomaly that rendered the theory unsatisfactory. Now there was freedom to choose the particular symmetry structure that one used in defining a theory in the first place. In fact, there were an infinite number of possibilities for these symmetry structures. However, for just one of them the anomaly magically cancelled out of the formulae, whereas for all the others it didn't. So amid this infinity of possibilities, just one unique one was being picked out as being potentially consistent.
If you were prepared to ignore the weird numbers 10 or 26, this discovery was very exciting. It suggested that there might be a mathematical reason for space-time to have a particular number of dimensions. It was
disappointing that the number was not four, but it was a start. Physicists had always wondered why space-time has the dimensions it does; now it looked as though there might be a better answer to that question than, “well, it could be anything, but in our universe it's four.”
Perhaps other theories would lead to a four-dimensional space-time. It would have been ideal, but nothing along those lines seemed to work, and the funny dimensions refused to go away. So maybe they were
there.
This was an old idea of Kaluza's: space-time might have extra dimensions that we are unable to observe. If so, the strings would remain one-dimensional loops, but those loops would vibrate in an otherwise invisible higher-dimensional space. The quantum numbers associated with the particles, like charge or charm, would be determined by the form of the vibrations.
A basic question was, what do the hidden dimensions look like? What
shape
is space-time?
At first, physicists hoped the extra dimensions would form some simple shape like the 6-dimensional analogue of a torus. But in 1985, Philip Candelas, Gary Horowitz, Andrew Strominger, and Witten reasoned that the most suitable shape would be a so-called CalabiâYau manifold. There are tens of thousands of these shapes; here is a typical one:

A CalabiâYau manifold (schematic).
Credit: Andrew J. Hanson, Professor and Chair, Indiana University.
Â
The great advantage of CalabiâYau manifolds is that the supersymmetry of 10-dimensional space-time is inherited by the ordinary four-dimensional space-time that underlies it.
For the first time, the exceptional Lie groups were taking on a prominent role in frontier physics, and this trend accelerated. Around 1990, there seemed to be five possible types of superstring theory, all with space-time dimension equal to 10. The theories are called Type I, Types IIA and IIB, and “heterotic” types HO and HE. Interesting gauge symmetry groups turn up; for example, in Types I and HO we find SO(32), the rotation group in 32-dimensional space, and in Type HE the exceptional
Lie group E
8
turns up as E
8
à E
8
, two distinct copies acting in two different ways.
The exceptional group G
2
also makes an appearance in the latest twist to the story, which Witten calls M-theory. The “M,” he says, stands for magic, mystery, or matrix. M-theory posits an 11-dimensional space-time, which unifies all five of the 10-dimensional string theories, in the sense that each can be obtained from M-theory by fixing some of its constants to particular values. In M-theory, CalabiâYau manifolds are replaced by 7-dimensional spaces known as G
2
-manifolds, because their symmetries are closely related to Killing's exceptional Lie group G
2
.

At the moment there is a bit of a backlash against string theory; not on the grounds that it is known to be wrong, but on the grounds that it's not yet known to be right. Several prominent physicists, especially experimentalists, have never had much truck with superstrings anywayâmostly because it didn't give them anything to
do.
There were no new phenomena to observe, no new quantities to measure.
I'm not wedded to superstrings as the key to the universe, but I think this criticism is unfair. String theorists are being asked to prove their innocence, whereas normally it would be up to the critics to prove their guilt. It takes a lot of time and effort to develop radically new ways of thinking about the physical world, and string theory is technically very difficult. In principle, it
can
make new predictions about our world; the big problem is that doing the necessary sums is extraordinarily hard. The same complaint could have been made about quantum field theory 40 years ago, but eventually the sums got done, through a combination of better computers and better mathematics, and the agreement with experiment turned out to be better than we find anywhere else in science.
Moreover, much the same charge can be leveled at almost any hopeful Theory of Everything, and paradoxically, the better it is, the harder it will be to prove correct. The reason is inherent in the nature of a Theory of Everything. In order to be successful, it must agree with quantum theory whenever it is applied to any experiment whose results are consistent with quantum theory. It must also agree with relativity whenever it is applied to any experiment whose results are consistent with relativity. So the Theory of Everything is obliged to pass
every experimental test yet devised.
Asking for a new prediction that distinguishes the Theory of Everything from
conventional physics is rather like asking for something that yields results identical to those predicted by theories describing all known physical phenomena, yet is different.
Of course, eventually string theory will have to make a new prediction, and be tested against observations, to make the transition from speculative theory to real physics. The need to agree with everything currently known does not rule out such predictions, it just explains why they don't come easily. Some tentative proposals for critical experiments already exist. For instance, recent observations of distant galaxies indicate that the universe is not only expanding, but expanding increasingly fast. Superstring theory offers a simple explanationâgravity is leaking away into those extra dimensions. However, there are other ways to explain this particular effect. What is clear is that if the theorists all stop investigating superstring physics, we will never have a chance to find out whether the theory is correct. It takes time and effort to come up with the crucial experiments, even if they exist.

I don't want to leave the impression that when it comes to unifying quantum theory with relativity, superstrings are the only game in town. There are many competing proposalsâthough they all suffer from the same lack of experimental support.
One idea, known as “noncommutative geometry,” is the brainchild of the French mathematician Alain Connes. It rests on a new concept of the geometry of space-time. Most unifications start with the idea that space-time is some extension of Einstein's relativistic model, and try to make the fundamental particles of subatomic physics fit in somehow. Connes does the opposite. He starts from a mathematical structure known as a non-commutative space, which contains all of the symmetry groups that arise in the standard model, and then deduces features similar to relativity. The mathematics of such spaces traces back to Hamilton and his noncommutative quaternions, but is extensively generalized and modified. Once again, though, this alternative theory is firmly rooted in Lie group theory.
Another intriguing idea is “loop quantum gravity.” In the 1980s, the physicist Abhay Ashtekar worked out how Einstein's equations would look in a quantum setting where space is “grainy.” Lee Smolin and Carlo Ravelli developed his ideas, leading to a model of space that is rather like medieval chain mailâconstructed from very tiny lumps about 10
â35
meters across, joined by links. They noticed that the detailed structure of the chain mail can get very complex as the links become knotted or braided together. However, it was not clear what these possibilities meant.
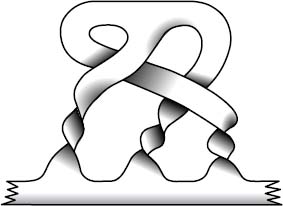
An electron represented as a braid.
In 2004, Sundance Bilson-Thompson discovered that some of these braids exactly reproduce the rules for combining quarks. The electric charge of the quark is reinterpreted in terms of the topology of the associated braid, and the combination rules follow from simple geometric operations with braids. This idea, still in its infancy, produces most of the particles observed in the standard model. It is the latest in a series of speculative proposals that matterâhere realized as particlesâmight be a consequence of “singularities” in space, such as knots, localized waves, or more complicated structures where space ceases to be smooth and regular. If Bilson-Thompson is right, matter is just twisted space-time.
Mathematicians have been studying the topology of braids for many years and have long known that braids themselves form a group, the
braid group.
The operation of “multiplication” arises when two braids are joined end to endâmuch as we joined permutations end to end when discussing Ruffini's approach to the quintic. Yet again, physics is building on preexisting mathematical discoveries, mostly made “for their own sake” because they looked interesting. And yet again, a key ingredient is symmetry.

