Why Beauty is Truth (52 page)

This isn't such a silly idea. If you look at a hosepipe from a distance, the pipe looks like a curve, which is one-dimensional. Only from close up does it become clear that the pipe is really three-dimensional, with a small two-dimensional cross-section. This hidden structure in new dimensions explains something that you
can
observe from a distance: how the hose is able to carry water. The cross-section just needs to have the right shape, with a central hole. Now imagine that the thickness of the hose is less than the size of an atom. You would have to look extraordinarily closely to notice the extra dimensions. The incredibly thin hosepipe would no longer be able to carry water, but anything sufficiently small could still travel along it.

So it may be possible to perceive the effect of extra dimensions without perceiving the dimensions themselves. That means that hidden dimensions of space-time are an entirely scientific suggestion: their presence can in principle be tested—but by inference, rather than by a direct use of the senses. Most scientific tests work by inference—if you could see the cause of some phenomenon directly, you wouldn't need theories or experiments. No one has ever seen an electromagnetic field, for example. They
have seen sparks and watched compass needles swing to point north, and (if they are scientists) they have inferred that a field must be responsible.

Kaluza's theory gained a certain popularity because it was the only known idea that held out hope of a unified field theory. In 1926, another mathematician, Oskar Klein, improved Kaluza's theory with the suggestion that quantum mechanics might explain why that fifth dimension curled up so tightly. In fact, its size should be of a similar order of magnitude to Planck's constant: the “Planck length” of 10
^–35
meters.

For a while, physicists were attracted to Kaluza–Klein theory, as it became known. But the impossibility of
directly
demonstrating the presence of that extra dimension preyed on their minds. By definition, Kaluza–Klein theory was consistent with every known phenomenon in gravitation and electromagnetism. You could never disprove it with standard experiments. But it didn't really add anything; it didn't predict anything new that could be tested. The same problem bedevils many attempts to unify existing laws. What's testable is already known, and what's new isn't testable. The initial enthusiasm began to wane.

The deathblow for Kaluza–Klein theory—not whether it was right, but whether it was worth spending precious research time on—was the explosive growth of a much sexier theory, one in which you really could make new predictions and do experiments to test them. This was quantum theory, then in its first flush of youth.

By the 1960s, though, quantum mechanics was running out of steam. Early progress had given way to deep puzzles and inexplicable observations. Quantum theory's success was undeniable, and it would shortly lead to the “standard model” of fundamental particles. But it was becoming ever more difficult to find new questions that had any chance of being answered. Genuinely novel ideas were too hard to test; testable ideas were mere extensions of existing ones.

One very elegant underlying principle had emerged from all the research: the key to the structure of matter on very tiny scales is
symmetry.
But the important symmetries for fundamental particles are not the rigid motions of Euclidean space, not even the Lorentz transformations of relativistic space-time. They include “gauge symmetries” and “supersymmetries.” And there are other kinds of symmetry, too, more like the symmetries studied by Galois, which act by permuting a discrete set of objects.

How can there be different kinds of symmetry?

Symmetries always form a group, but there are many different ways in which a group can
act.
It might act by rigid motions such as rotations, by permuting components, or by reversing the flow of time. Particle physics led to the discovery of a new way for symmetries to act, called gauge symmetries. The term is a historical accident, and a better name would be
local
symmetries.

Suppose that you are traveling in another country—let us call it Duplicatia—and you need money. The Duplicatian currency is the pfunnig, and the exchange rate is two pfunnigs to the dollar. You find this confusing until you notice a very simple and obvious rule for translating dollar transactions into pfunnigs. Namely, everything costs twice as many pfunnigs as you would expect to pay in dollars.

This is a kind of symmetry. The “laws” of commercial transactions are unchanged if you double all the numbers. To compensate for the numerical difference, though, you have to pay in pfunnigs, not in dollars. This “invariance under change of monetary scale” is a
global
symmetry of the rules for commercial transactions. If you make the same change throughout, the rules are invariant.

But now . . . Just across the border, in neighboring Triplicatia, the local currency is the boodle, and these are valued at three to the dollar. When you take a day trip to Triplicatia, the corresponding symmetry requires all sums to be multiplied by
three.
But again the laws of commerce remain invariant.

Now we have a “symmetry” that differs from one place to another. In Duplicatia, it is multiplication by two; in Triplicatia, by three. You would not be surprised to find that on visiting Quintuplicatia the corresponding multiple is five. All of these symmetry operations can be applied simultaneously, but each is valid only in the corresponding country. The laws of commerce are still invariant, but only if you interpret the numbers according to the correct local currency.

This local rescaling of currency transactions is a gauge symmetry of the laws of commerce. In principle, the exchange rate could be different at every point of space and time, but the laws would still be invariant provided you interpreted all transactions in terms of the local value of the “currency field.”

Quantum electrodynamics combines special relativity and electromagnetism. It was the first physical unification since Maxwell's, and it is based on a gauge symmetry of the electromagnetic field.

We have seen that electromagnetism is symmetric under the Lorentz group of special relativity. This group consists of global space-time symmetries; that is, its transformations must be applied consistently throughout the entire universe if we want to preserve Maxwell's equations. However, Maxwellian electromagnetism also has a gauge symmetry, which is vital to quantum electrodynamics. This symmetry is a
change of phase
in light.

Any wave consists of regular wobbles. The maximum size of the wobble is the amplitude of the wave. The time at which the wave hits that maximum is called its
phase
; the phase tells you when and where the peak value occurs. What really matters is not the absolute phase of any given wave but the difference in phases between two distinct waves. For example, if the phase difference of two otherwise identical waves is half the period (the time between maximum heights), then one wave hits its maximum exactly out of step with the other one, so the peaks of one coincide with the troughs of the other.

When you walk along the street, you left foot is half a period out of phase with your right foot. When an elephant walks along the street, successive feet hit the ground at phases 0, ¼, ½, and ¾ of the full period; first the left rear, then the left front, then the right rear, then the right front. You can appreciate that if we started counting from 0 at a different foot, we would get different numbers—but the phase
differences
would still be 0, ¼, ½, and ¾. So relative phases are well defined and physically meaningful.

Suppose a beam of light is passing through some complicated system of lenses and mirrors. The way it behaves turns out not to be sensitive to the overall phase. A change of phase is equivalent to a small time delay in making observations, or a resetting of the observer's clock. It does not affect the geometry of the system or the path of the light. Even if two light waves overlap, nothing changes, provided both waves have their phases shifted by the same amount.

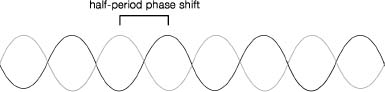
Effect of a phase shift on a wave.

So far, “change phase” is a global symmetry. But if an alien experimentalist somewhere in the Andromeda Galaxy changed the phase of light in one of its experiments, we would not expect to notice any effect inside a terrestrial laboratory. So the phase of light can be changed at will at all locations in space and time, and the laws of physics should remain invariant. The possibility of changing the phase arbitrarily at each point of space-time, with no global constraint to make the same change everywhere, is a gauge symmetry of Maxwell's equations, and it carries over into the quantum version of those equations, quantum electrodynamics.

A phase shift of a full vibrational period is the same as no phase shift at all, and this implies that in the abstract, changing phase is a
rotation.
So the symmetry group involved here—the “gauge group”—is SO(2), the rotation group in two dimensions. However, physicists like their quantum coordinate transformations to be “unitary”—defined by complex numbers, not real ones. Fortunately, SO(2) has another incarnation as the unitary group U(1)—rotations in the
complex
plane.

In short: quantum electrodynamics has U(1) gauge symmetry.

Gauge symmetries were the clue to the next two unifications of physics, the electroweak theory and quantum chromodynamics. Together these constitute the “standard model,” the currently accepted theory of all fundamental particles. Before we can see how this goes, we must explain exactly what is being unified: not theories but
forces.

Today's physics recognizes four distinct kinds of force in nature: gravity, electromagnetism, the weak nuclear force, and the strong nuclear force. They have very different characteristics: they operate on different scales of space and time, some cause particles to attract each other, some cause them to repel each other, some do both depending on the particles, and some do both depending on how far apart the particles are.