Why Beauty is Truth (55 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

How four species diverge as time passes.
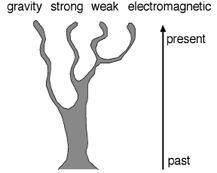
How the four fundamental forces diverge as time passes.
When the universe first came into being at the Big Bang, 13 billion years ago, it was enormously hot. At first, all four forces acted in exactly the same way. But as the universe cooled, its symmetry broke, and the forces split into individuals with distinguishable characteristics. Our present universe, with its four forces, is an imperfect shadow of that elegant originalâthe result of three broken symmetries.
THE POLITICAL JOURNALIST
I
n June 1972, during the run-up to the U.S. presidential election, a security guard at the Watergate complex noticed that a door had been taped open. He removed the tape, thinking it must have been left accidentally by workmen, but when he returned, someone had put it back. His suspicions aroused, the guard informed the police, who caught five men breaking into the offices of the Democratic Party's national committee. It turned out that the men were associated with President Nixon's reelection committee.
The discovery had little effect on the election itself; Nixon won in a landslide. But the story wouldn't go away, and slowly the tentacles of the Watergate affair reached higher and higher in the Nixon administration. Two reporters from the
Washington Post
, Bob Woodward and Carl Bernstein, pursued the story with dogged persistence, assisted by the clandestine revelations of “Deep Throat.” No one knew who he was, but it was clear that he had to be a very senior official. In 2005, Deep Throat was revealed as Mark Felt, the second-in-command in the Federal Bureau of Investigation.
The information that Deep Throat leaked to the press was dynamite. By April 1974, Nixon had been forced to ask for the resignations of two senior aides. Then it turned out that the president had bugged his own office, and there were recorded tapes of sensitive conversations. After a legal battle to secure access to the tapes, gaps were found in some of the recordings, apparently the result of deliberate erasure.
The attempt to cover up the relation between the burglary and the White House was almost universally perceived as a worse crime than the burglary itself. The House of Representatives began a formal process that could lead
to the president being impeachedâtried for “high crimes and misdemeanors” before the U.S. Senate, and if found guilty, removed from office. When impeachment and conviction became inevitable, Nixon resigned.
Nixon's opponent in the election was Senator George McGovern. Announcing his candidacy for the Democratic nomination in Sioux Falls, South Dakota, McGovern made some prophetic remarks:
Today, our citizens no longer feel that they can shape their own lives in concert with their fellow citizens. Beyond that is the loss of confidence in the truthfulness and common sense of our leaders. The most painful new phrase in the American political vocabulary is “credibility gap”âthe gap between rhetoric and reality. Put bluntly, it means that people no longer believe what their leaders tell them.
Among the minor figures in McGovern's campaign was a would-be political journalist whose career would probably have taken off had Mc-Govern been elected. In that variant of history, politics might have been richer, but fundamental physics and advanced mathematics would have been much the poorer. In the year 2004 of the history that actually happened, the journalist was listed by
Time
magazine as one of the year's one hundred most influential peopleâbut not for his journalism.
Instead, he was listed for his groundbreaking contributions to mathematical physics. He is responsible for some of the most original mathematics in the worldâfor which he won the Fields Medal, the top honor in mathematics, comparable in prestige to a Nobel Prizeâbut he is not a mathematician. He is one of the world's leading theoretical physicists, and was awarded the National Medal of Science, but his first degree was in history. And he is the prime mover, though not quite the original creator, of the current front-runner in the effort to unify the whole of physics. He is the Charles Simonyi professor of mathematical physics at the Institute for Advanced Study in Princeton, where Einstein used to work, and his name is Edward Witten.
Like the great German quantum theorists but unlike poor Dirac, Witten grew up in an intellectual environment. His father, Louis Witten, is also a physicist, working on general relativity and gravitation. Edward was born in Baltimore, Maryland, and studied for his first degree at Brandeis University. After Nixon's reelection, he went back to academic life, taking
a PhD at Princeton University, and embarked on a career of research and teaching at various American universities. In 1987 he was appointed to the Institute for Advanced Study, where all academic positions focus purely on research, and this is where he currently works.
Witten started research in quantum field theory, the first fruits of efforts to reconcile quantum theory with relativity. Here relativistic effects of motion are taken into account, but only in flat space-time. (Gravity, which requires curved space-time, is not considered.) In 1998, in a Gibbs lecture, Witten said that quantum field theory “encompasses most of what we know of the laws of physics, except gravity. In its seventy years there have been many milestones, ranging from the theory of âantimatter' . . . to a more precise description of atoms . . . to the âstandard model of particle physics.'” He pointed out that having been developed largely by physicists, much of it lacked mathematical rigor and so had had little impact on mathematics as such.
The time was ripe, Witten said, to remedy that shortcoming. Several major areas of pure mathematics were effectively quantum field theory in disguise. Witten's own contribution, the discovery and analysis of “topological quantum field theories,” had a direct interpretation in terms of concepts that various pure mathematicians had invented in quite different settings. These included the English mathematician Simon Donaldson's epic discovery that four-dimensional space is unique in supporting many different “differentiable structures”âcoordinate systems in which calculus can be carried out. Other aspects are a recent breakthrough in knot theory, known as the Jones polynomial, a phenomenon called “mirror symmetry” in multidimensional complex surfaces, and several areas of modern Lie theory.
Witten made a bold prediction: a major theme in twenty-first-century mathematics would be the integration of ideas from quantum field theory into the mathematical mainstream:
One has here a vast mountain range, most of which is still covered with fog. Only the loftiest peaks, which reach above the clouds, are seen in the mathematical theories of today, and these splendid peaks are studied in isolation . . . Still lost in the mist is the body of the range, with its quantum field theory bedrock and the great bulk of the mathematical treasures.
Witten's Fields Medal celebrated his uncovering of a few of those hidden treasures. Among them was a new and improved proof of the “positive mass conjecture,” to the effect that a gravitational system with positive local mass density must have positive total mass. It may sound obvious, but in the quantum world mass is a subtle concept. The proof of this long-sought result, published by Richard Schoen and Shing-Tung Yau in 1979, had earned Yau a Fields Medal in 1982. Witten's new, improved proof exploited “supersymmetry,” the first application of that concept to a significant problem in mathematics.

We can understand supersymmetry in terms of an old puzzle, which asks for a cork that can fit into a bottle whose opening may be circular, square, or triangular. Amazingly, such shapes do exist, and the traditional answer is a cork with a circular base that tapers like a wedge. Viewed from below, it looks like a circle; viewed from the front it is a square; viewed from the side it is a triangle. A single shape can perform all three tasks because a three-dimensional object can have several different “shadows,” or projections, in different directions.
Now, imagine a Flatlander living on the “floor” of my picture, able to observe the projection of the cork onto the floor but unaware of the other projections. One day he discovers to his amazement that the circular shape has somehow morphed into a square. How can that be? It's certainly not a symmetry.
Not in Flatland. But while the Flatlander's back was turned, someone living in three dimensions rotated the cork so that its projection onto the floor changed to a square. And rotation
is
a symmetry transformation in three dimensions. So a symmetry in a higher dimension can sometimes explain a rather baffling transformation in a lower dimension.
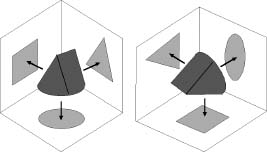
How supersymmetry works. Left: A cork to fit three shapes of hole. Right: Effect of rotating the cork.
Something very similar happens in supersymmetry, but instead of changing circles into squares, it changes fermions into bosons. This is amazing. It means that you can do calculations with fermions, hit everything with a supersymmetry operation, and deduce results for bosons with no extra effort. Or the other way round.
We expect this kind of thing to happen with genuine symmetries. If you stand in front of a mirror and juggle several balls, then whatever happens on your side of the mirror completely determines what happens on the other side. There, an image of you juggles images of the balls. If it takes 3.79 seconds to complete one sequence of juggles on the real side of the mirror, you know without doing the measurements that it will also take 3.79 seconds to complete the corresponding sequence of juggles on the other side. The two situations are related by a reflectional symmetry; whatever happens in one also happens, reflected, in the other.
Supersymmetries are not as obvious as this, but they have a similar effect. They let us deduce features of one type of particle from features of an entirely different type of particle. It is almost as if you could reach into some higher-dimensional region of the universe and twist a fermion into a boson. Particles come in supersymmetric pairs: an ordinary particle is matched with its twisted version, called a sparticle. Electrons are paired with selectrons, quarks with squarks. For historical reasons the photon is twinned not with the sphoton but with the photino. There is a kind of “shadow world” of sparticles that interacts only weakly with the ordinary world.
This idea makes for elegant mathematics, but the masses of these predicted shadow particles are too great for them to be observed in experiments. Supersymmetry is beautiful, but it may not be true. But even though direct confirmation is out of the question, indirect confirmation is still possible. Science mainly checks theories through their implications.

