Why Beauty is Truth (56 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

Witten pursued supersymmetry vigorously, and in 1984 he wrote an article titled “Supersymmetry and Morse theory.” Morse theory is an area of topology, named for the pioneer Marston Morse, that relates the overall shape of a space to its peaks and valleys. Sir Michael Atiyah,
probably Britain's most distinguished living mathematician, described Witten's paper as “obligatory reading for geometers interested in understanding modern quantum field theory. It also contains a brilliant proof of the classic Morse inequalities . . . The real aim of the paper is to prepare the ground for supersymmetric quantum field theory [in terms of] infinite-dimensional manifolds.” Subsequently, Witten applied these techniques to other hot topics at the frontiers of topology and algebraic geometry.
It should be obvious that when I said Witten is not a mathematician, I did not mean he lacks mathematical abilityâquite the reverse. Arguably no one on the planet has more mathematical ability. But in Witten's case it is complemented by an amazing physical intuition.
Unlike mathematicians, physicists are seldom shy about employing physical intuition to paper over any gaps in mathematical logic. Mathematicians have learned to regard leaps of faith with suspicion, however strong the supporting evidence may be: to them, proof is all. Witten is unusual in that he can relate his intuition to mathematics as mathematicians understand it. Atiyah puts it like this: “His ability to interpret physical ideas in mathematical form is quite unique. Time and again he has surprised the mathematical community by his brilliant application of physical insight leading to new and deep mathematical theorems.”
But there is a flipside to this intuitive prowess. Many of Witten's most important ideas, being derived from physical principles or analogies, were arrived at without proofs, and some still lack proofs today. It's not that he can't
do
proofsâas his Fields Medal demonstratesâbut he can make leaps of logic that lead to deep and correct mathematics without seeming to need proofs.

The big question is, does Witten's wonderfully elegant mathematics have anything to do with fundamental physics? Or has the search for beauty headed down a mathematical dead end, losing any connection with physical truth?
By 1980, physicists had unified three of the four forces of nature: electromagnetic, weak, and strong. But Grand Unified Theories said nothing about gravity. The force that we experience most directly in everyday life, which literally keeps our feet on the ground, was embarrassingly absent from the synthesis.
It was easy enough to write down combined theories of gravity and quantum theory that looked sensible. But whenever anyone tried to solve the resulting equations, they got nonsense. Typically, numbers that ought to represent reasonable physical quantities were infinite. An infinity in a physical theory is a sign that something is wrong. It was an infinity in the radiation law that inspired Planck to quantize light.
Some physicists became convinced that the main source of the infinities was the ingrained habit of treating particles as points. A pointâlocation without sizeâis a mathematical fiction. Quantum particles were probabilistic fuzzed-out points, but that didn't cure the disease; something more drastic was needed. Even in the 1970s a few pioneers had begun to think that particles might more sensibly be modeled as tiny vibrating loopsâ“strings.” In the 1980s, when supersymmetry got in on the act, these mutated into
superstrings.
One could write an entire book about superstrings, and several people have, but we can manage with a rough hand-waving description. I want to focus on four features: the way relativistic and quantum pictures are combined, the need for extra dimensions, the interpretation of quantum states as vibrations in those extra dimensions, and the symmetries of the extra dimensionsâor, more accurately, of various fields that live in them.
Our starting point is Einstein's idea of representing the trajectory of a particle in space-time as a curve, which he called its
world line.
Essentially, this is the curve that the particle traces in space-time as it moves. In relativity, world lines are smooth curves, because of the form of Einstein's field equations. They do not branch, because in relativity the future of any system is completely determined by its past, indeed by its present.
There is an analogous concept in quantum field theory called a Feynman diagram. Feynman diagrams depict the interaction of particles in a rather schematic space-time. For example, the left-hand picture (next page) is the Feynman diagram for an electron that emits a photon that is then captured by a second electron. It is traditional to use wiggly lines for photons.
The Feynman diagram is a bit like a relativistic world line, but it has sharp corners and it branches. In 1970, it occurred to Yoichiro Nambu that if the assumption that particles are points is replaced by the assumption that they are tiny loops, then Feynman diagrams can be converted into smooth surfacesâ
worldsheets
âas in the right-hand picture. A worldsheet can be interpreted as a world line in a modified space-time, with an extra dimension for the loops to live in.
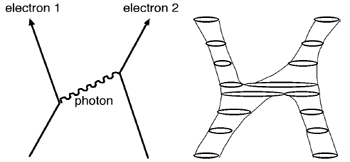
(Left) Feynman diagram for interacting particles. (Right) The corresponding worldsheet, sliced into strings.
The great thing about loopsâaside from not being pointsâis that they can vibrate. Perhaps each vibrational pattern corresponded to a quantum state. That would explain why quantum states come in whole-number multiples of some basic quantityâfor example spin, which is always an integer multiple of ½. The number of waves that fit into the loop has to be a whole number. In a violin string, these different patterns are the fundamental note and its higher harmonics. So quantum theory becomes a kind of music, played with superstrings instead of violin strings.
Nambu's idea did not come out of the blue. It had its roots in a remarkable formula derived by Gabriele Veneziano in 1968, which showed that apparently distinct Feynman diagrams represent the same physical process, and that any failure to take that into account leads to wrong answers in quantum field theory calculations. Nambu noticed that when the Feynman diagram is surrounded by tubes, different diagrams yield networks of tubes with the same topology. That is, these networks can be deformed into each other. So Veneziano's formula seemed to be related to the topological properties of the tubes.
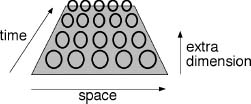
Strings poke out of ordinary space-time into new dimensions.
This, in turn, hinted that quantum particles, with their discrete quantum numbers like charge, might be topological features of a smooth space-time. Mathematicians had already observed the tendency of basic topological propertiesâsuch as the number of holes in a surfaceâto be discrete. It all seemed to fit. But as always, the devil was in the detail, and the detail was devilish. String theory was the first attempt to get the detail in agreement with the real world.

String theory did not start out as a possible route to a Theory of Everything but as a proposal to explain the particles collectively known as hadrons. These include most of the common particles found in the atomic nucleus, such as the proton and neutron, together with a host of more exotic particles. However, the theory had a flaw: it predicted the existence of a particle with zero mass and spin 2, which had never been observed (and still hasn't). Additionally, it failed to predict any particles with spin ½âand rather a lot of hadrons, including the proton and neutron, have spin ½. It was like a midsummer weather forecast that predicts hailstones a foot across but has nothing to say about whether the temperature will be warm. Physicists were unimpressed. In 1974, when quantum chromodynamics came along and explained all known hadrons, and even successfully predicted a new one, the omega-minus, the fate of string theory seemed sealed.
At that point, however, John Schwarz and Joel Scherk noticed that string theory's unwanted zero-mass spin-2 particle might be the long-sought graviton, the hypothetical particle believed to carry the force of gravity. Might string theory be a quantum theory of
gravity
, rather than hadrons? If so, it would be an attractive contender for a Theory of Everythingâwell, for a Theory of Many Things, because there are many particles that are not hadrons.
At this point, supersymmetry came into play, because it converts fermions into bosons. Hadrons include particles of both kinds, but other particles, such as the electron, are not hadrons. If supersymmetry could be incorporated into string theory, then a number of new particles would automatically come within the theory's graspâcarried along by super-symmetric partners that were already part of the theory.
The combined theory, developed by Pierre Ramond, André Neveu, and Schwarz, was superstring theory. This theory did include spin-½ particles, and it eliminated a nasty feature of ordinary string theory, a particle that
goes faster than light. The presence of such a particle in a theory is now seen as evidence that it is unstable, which rules it out.
From 1980 onward, Michael Green, a British theoretical physicist, worked out more and more of the mathematics of superstrings, using techniques from Lie group theory and topology, and it quickly became clear that whatever its physical credentials, superstring theory possessed extraordinary mathematical beauty. The physics remained obstinate: in 1983, Luis Alvarez-Gaume and Witten discovered a new snag with string theories, including superstrings and even good old quantum field theory. Namely, these theories normally possess
anomalies.
An anomaly occurs when the process of converting a classical system to its quantum analogue changes an important symmetry.
Green and Schwarz had discovered that very occasionally, the anomalies miraculously disappear, but only if space-time has 26 dimensions (in the first version of the theory, called bosonic string theory) or 10 dimensions (in later modifications). Why? In their calculations for bosonic string theory, the mathematical terms that would create an anomaly are multiplied by
d
â 26, where
d
is the dimension of space-time. So these terms vanish precisely when
d
= 26. Similarly, in the modified version, the factor becomes
d
â10. Time always remains one-dimensional, but space somehow acquires an extra 6 or 22 dimensions. Schwarz put it this way:
