Why Beauty is Truth (27 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart


So far, the interpretation of groups as symmetries has been somewhat metaphorical. Now we need to make it more literal, and that step requires a more geometric point of view. Galois's successors quickly realized that the relation between groups and symmetry is much easier to understand in the context of geometry. In fact, this is how the subject is usually introduced to students.
To get a feeling for this relationship, we'll take a quick look at my favorite group: the symmetry group of an equilateral triangle. And we'll finally address a very basic question: What, exactly,
is
symmetry?
Before Galois, all answers to this question were rather vague, handwavy things, with appeals to features like elegance of proportion. This is not a concept you can do sensible mathematics with. After Galoisâand after a short period during which the world of mathematics sorted out the general ideas behind his very specific applicationâthere was a simple and unequivocal answer. First, the word “symmetry” has to be reinterpreted as “
a
symmetry.” Objects do not possess symmetry alone; they often possess many different symmetries.
What, then, is a symmetry? A symmetry of some mathematical object is a transformation that preserves the object's structure. I'll unpack this definition in a moment, but the first point to observe is that a symmetry is a process rather than a thing. Galois's symmetries are permutations (of the roots of an equation), and a permutation is
a way to rearrange things.
It is not, strictly speaking, the rearrangement itself; it is the rule you apply to get the rearrangement. Not the dish but the recipe.
This distinction may sound like splitting hairs, but it is fundamental to the whole enterprise.
There are three key words in the definition of a symmetry: “transformation,” “structure,” and “preserve.” Let me explain them using the example of an equilateral triangle. Such a triangle is defined as having all three sides the same length and all three angles the same size, namely 60°. These features make it difficult to distinguish one side from another; phrases like “the longest side” don't tell us anything. The angles are also indistinguishable. As we now see, the inability to distinguish one side from another or one angle from another is a consequence of the
symmetries of the equilateral triangle. In fact, it is what defines those symmetries.
Let's consider those three words in turn.
Transformation:
We are allowed to do things to our triangle. In principle there are lots of things we might do: bend it, turn it through some angle, crumple it up, stretch it like elastic, paint it pink. Our choice here is more limited, however, by the second word.
Structure:
The structure of our triangle consists of the mathematical features that are considered significant. The structure of a triangle includes such things as “it has three sides,” “the sides are straight,” “one side has length 7.32 inches,” “it sits in the plane at this location,” and so on. (In other branches of mathematics, the significant features may be different. In topology, for instance, what matters is that the triangle forms a single closed path, but its three corners and the straightness of its edges are no longer important.)
Preserve:
The structure of the transformed object must match that of the original. The transformed triangle must also have three sides, so crumpling it is ruled out. The sides must remain straight, so bending it is not permitted. One side must still have length 7.32 inches, so stretching the triangle is forbidden. The location must be the same, so sliding it ten feet sideways is disallowed.
The color is not explicitly mentioned as structure, so painting the triangle pink is irrelevant. It's not exactly ruled out; it just makes no difference for geometric purposes.
Turning the triangle through some angle, however, does preserve at least some of the structure. If you make an equilateral triangle out of cardboard, set it on the table, and then rotate it, it still looks like a triangle. It has three sides, they are still straight, their lengths haven't changed. But the location of the triangle in the plane may still look different, depending on the angle through which you rotate it.
If I turn the triangle through a right angle, for instance, the result looks different. The sides point in different directions. If you covered your eyes while I turned the triangle, you would know when you opened them again that I had moved it.
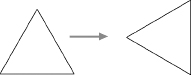
Rotation through a right angle is not a symmetry of the equilateral triangle.
But if I turned the triangle through 120°, you wouldn't be able to see any difference between “before” and “after.” To show you what I mean, I will secretly mark the corners with different types of dots, so we can see where it moves to. These dots are for reference only and are not part of the structure that is preserved. If you can't see the dots, if the triangle is as featureless as any well-behaved Euclidean object, then the turned triangle looks the same as the original.
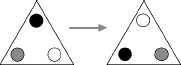
Rotation through 120° is a symmetry of the equilateral triangle.
In other words, “rotate by 120°” is a symmetry of the equilateral triangle. It is a transformation (“rotate”) that preserves the structure (shape and location).
It turns out that an equilateral triangle has precisely six different symmetries. Another is “rotate by 240°.” Three more are reflections, which turn the triangle over so that one corner remains fixed and the other two exchange positions. What is the sixth symmetry?
Do nothing.
Leave the triangle alone. This is trivial, but it fits the definition of symmetry. In fact, this transformation fits the definition of symmetry no matter what object we consider or what structure we want preserved. If you do nothing, then nothing changes.
This trivial symmetry is called the
identity.
It may seem insignificant, but if we leave it out, the math gets very messy. It's like trying to do addition without the number zero or multiplication without the number one. If we keep the identity in, everything stays neat and tidy.
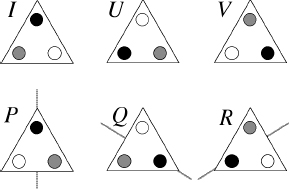
The six symmetries of the equilateral triangle.
For the equilateral triangle, you can think of the identity as rotation through 0°. On the previous page are the results of applying the six symmetries to our equilateral triangle. They are precisely the six different ways that you can pick up a triangle made of cardboard and lay it down within its original outlines. The dotted lines show where to put the mirror to obtain the required reflection.
Now I want to convince you that symmetries are a part of algebra. So I will do what any algebraist would do: express everything in terms of symbols. We will name the six symmetries
I, U, V, P, Q, R
according to the picture above. The identity is
I;
the other two rotations are
U
and
V;
the three reflections are
P, Q
, and
R.
These are the same symbols that I used earlier for permutations of the roots of a cubic. There is a reason for this duplication, which will shortly emerge.
Galois made great play of the “group property” of his permutations. If you perform any two in turn, you get another one. This provides a big hint about what we should do with our six symmetries. We should “multiply” them in pairs and see what happens. Recall the convention: if
X
and
Y
are two symmetry transformations, then the product
XY
is what happens when we first do
Y
, then
X.
Suppose, for instance, that we want to work out
VU.
This means that first we apply
U
to the triangle, then
V.
Well,
U
rotates it through 120°, and
V
then rotates the resulting triangle through 240°. So
VU
rotates it through 120° + 240° = 360°.
Oops, we forgot to include that.
No we didn't. If you rotate a triangle through 360°, everything ends up exactly where it started. And in group theory it is the end result that matters, not the route taken to get there. In the language of symmetries, two symmetries are considered to be the same if they have the same final effect on the object. Since
VU
has the same effect as the identity, we conclude that
VU
=
I.
For a second example, what does
UQ
do? The transformations go like this:
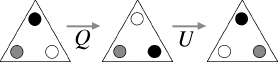
How to multiply symmetries.
We recognize the end result: it is
P.
So
UQ
=
P.
With our six symmetries we can form 36 products, and the calculations can be captured in a multiplication table. It is exactly the same table that we obtained for the six permutations of the roots of a cubic.

