Why Beauty is Truth (26 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

Working out precisely which permutations are symmetries of a given equation is a difficult technical exercise. But there is one thing we can be sure of without doing any calculations at all. The collection of all symmetries of a given equation must be a subgroup of the group of all permutations of the roots.
Why? Suppose, for instance, that both
P
and
R
preserve all algebraic relations among the roots. If we take some relation and then apply
R
, we get a valid relation. If we then apply
P
, we again get a valid relation. But applying
R
and then
P
is the same as applying
PR.
So
PR
is a symmetry. In other words, the collection of symmetries has the group property.
This straightforward fact underlies the whole of Galois's work. It tells us that associated with any algebraic equation there is a group, its symmetry groupânow called its
Galois group
to honor the inventor. And the Galois group of an equation is always a subgroup of the group of all permutations of the roots.
From this key insight a natural line of attack emerges. Understand which subgroups arise in which circumstances. In particular, if the equation can be solved by radicals, then the Galois group of the equation should reflect this fact in its internal structure. Then, given any equation, you just work out its Galois group and check whether it has the required structure, and you know whether it can be solved by radicals.

Now Galois could recast the whole problem from a different viewpoint. Instead of building a tower with ladders and sacks, he grew a tree.
Not that he called it a tree, any more than Abel talked of Cardano Tower, but we can picture Galois's idea as a process that repeatedly branches from a central trunk. The trunk is the Galois group of the equation. The branches, twigs, and leaves are various subgroups.
Subgroups arise naturally as soon as we start thinking about how the symmetries of equations change when we start taking radicals. How does the group change? Galois showed that if we form a
p
th root, then the symmetry group must split into
p
distinct blocks, all the same size. (Here, as Abel noted, we can always assume
p
to be prime.) So, for example, a group of 15 permutations might split into five groups of 3, or three groups of 5. Crucially, the blocks have to satisfy some very precise conditions; in particular, one of them must form a subgroup in its own right of a special kind known as a “normal subgroup of index
p.
” We can think of the trunk of the tree splitting into
p
smaller branches, one of which corresponds to the normal subgroup.
The normal subgroups of the group of all six permutations of three symbols are the entire group [
I, U, V, P, Q, R
], the subgroup [
I, U, V
], whose table we saw just now, and the subgroup with just one permutation, [
I
]. The other three subgroups, which contain two permutations, are not normal.
For instance, suppose we want to solve the general quintic. There are five roots, so the permutations involve five symbols. There are precisely 120 such permutations. The coefficients of the equation, being fully symmetric, have a group that contains all 120 of these. This group is the trunk of the tree. Each root, being totally asymmetric, has a group that contains just
one
permutationâthe trivial one. So the tree has 120 leaves. Our aim is to join the trunk to the leaves by branches and twigs whose structure reflects the symmetry properties of the various quantities that arise if we start working out the bits and pieces of a formula for the roots, which we assume are expressed by radicals.
Suppose for the sake of argument that the first step in the formula is to adjoin a fifth root. Then the group of 120 permutations must split into five pieces, each containing 24 permutations. So the tree develops five branches. Technically, this branching must correspond to a normal subgroup of index 5.
However, Galois could prove, merely by calculating with permutations, that
there does not exist such a normal subgroup.
Very well, perhaps the solution starts with, say, a seventh root. Then the 120 permutations must split into seven blocks of equal sizeâbut they can't, because 120 is not divisible by 7. No seventh roots, then. In fact, no prime roots except 2, 3, and 5, because those are the prime factors of 120. And we've just ruled out 5.
A cube root to start with, then? Unfortunately not: the group of 120 permutations has no normal subgroup of index 3.
All that's left is a square root. Does the group of 120 permutations have a normal subgroup of index 2? Indeed it does, precisely one. It contains 60 permutations, and is called the
alternating group.
So by using Galois's theory of groups, we have established that any formula for solving a general quintic must start with a square root, leading to the alternating group. The first place where the trunk splits leads to just two branches. But there are 120 leaves, so the branches must split again. How do the branches split?
The prime divisors of 60 are also 2, 3, and 5. So each of our new branches must split into two, three, or five twigs. That is, we must either adjoin another square root, a cube root, or a fifth root. Moreover, this can be done if and only if the alternating group has a normal subgroup of index 2, 3, or 5.
But does it have such a normal subgroup? That is a question purely about permutations of five symbols. By analyzing such permutations, Galois was able to prove that the alternating group
has no normal subgroups at all
(except for the whole group and the trivial subgroup [
I
]). It is a “simple” groupâone of the basic components out of which all groups can be constructed.
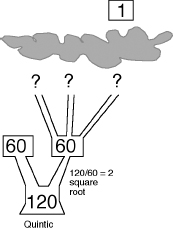
Galois's proof that the quintic is unsolvable.
There are too few normal subgroups to connect the trunk to the leaves by means of splitting into a prime number of branches at each successive step. So the process of solving the quintic by radicals grinds to an abrupt halt after that first step of adjoining a square root.
There is nowhere else to go.
No tree
can climb from the trunk all the way up to the leaves, and therefore there is no formula for the roots in terms of radicals.
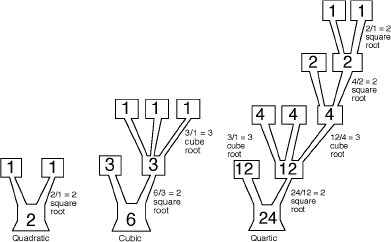
Using groups to solve the quadratic, cubic, and quartic.
The same idea works for equations of degree 6, 7, 8, 9âanything larger than 5. This leaves us wondering why the quadratic, cubic, and quartic
are
solvable. Why are degrees 2, 3, and 4 exceptional? In fact, group theory tells us exactly how to solve the quadratic, cubic, and quartic. I'll leave out the technicalities, and just show you the trees. They correspond precisely to the classical formulas.
Now we begin to see the beauty of Galois's idea. Not only does it prove that the general quintic has no radical solutions, it also explains why the general quadratic, cubic, and quartic
do
have radical solutions and tells us roughly what they look like. With extra work, it tells us
exactly
what they look like. Finally, it distinguishes those quintics that can be solved from those that can't, and tells us how to solve the ones that can.
The Galois group of an equation tells us everything we could possibly wish to know about its solutions. So why did Poisson, Cauchy, Lacroix, and all the other experts not leap with joy when they saw what Galois had done?
The Galois group has a terrible secret.

The secret is this. The easiest way to work out the group of an equation is to use properties of its roots. But of course, the whole point is that we usually do not know what the roots are. Remember, we are trying to solve the equation, that is, to find its roots.
Suppose someone presents us with a specific quintic, say
x
5
â 6
x
+ 3 = 0
or
x
5
+15
x
+ 12 = 0
and asks us to use Galois's methods to decide whether it can be solved by radicals. It seems a fair question.
The dreadful truth is that with the methods available to Galois,
there is no way to answer it.
We can assert that most likely, the associated group contains all 120 permutationsâand if it does, then the equation can't be solved. But we don't know for sure that all 120 permutations actually occur. Maybe the five roots obey some special constraint. How can we tell?
Beautiful though it may be, Galois's theory has severe limitations. It works not with the coefficients but with the roots. In other words, it works with the unknowns, not with the knowns.
Today, you can go to a suitable mathematical website, input your equation, and it will calculate the Galois group. We now know that the first equation above is not solvable by radicals, but the second one
is
solvable. My point is not the computer, but that someone has discovered what steps should be taken to solve the problem. The great advance since Galois in this area was working out how to compute the Galois group of any given equation.
Galois possessed no such technique. It would take another century before routine calculation of the Galois group became feasible. But the absence of this technique let Cauchy and Poisson off the hook. They could complain, with complete justification, that Galois's ideas did not solve the problem of deciding when a
given
equation could be solved by radicals.
What they failed to appreciate was that his method did solve a slightly different problem: to work out which properties of the
roots
made an equation solvable. That problem had an elegantâand deepâanswer. The problem they wanted him to solve . . . well, there is no reason to expect a
neat answer. There just isn't a tidy way to classify the solvable equations in terms of easily computed properties of their coefficients.
