Why Beauty is Truth (28 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

This apparent coincidence turns out to be an example of one of the most powerful techniques in the whole of group theory. It originated in the work of the French mathematician Camille Jordan, who arguably turned group theory into a subject in its own right, rather than just a method for analyzing the solution of equations by radicals.
Around 1870, Jordan drew attention to what is now called “representation theory.” To Galois, groups were composed of permutationsâways to shuffle symbols. Jordan started thinking about ways to shuffle more complicated spaces. Among the most basic spaces in mathematics are multidimensional spaces, and their most important feature is the existence of straight lines. The natural way to transform such spaces is
to keep straight lines straight.
No bending, no twisting. There are many transformations of this kindârotations, reflections, changes of scale. They are called “linear” transformations.
The English lawyer-mathematician Arthur Cayley discovered that any linear transformation can be associated with a
matrix
âa square table of numbers. Any linear transformation of three-dimensional space, for example, can be specified by writing down a 3-by-3 table of real numbers. So transformations can be reduced to algebraic computations.
Representation theory lets you start with a group that does not consist of linear transformations and replace it with one that does. The advantage of converting the group to a group of matrices is that matrix algebra is very deep and powerful, and Jordan was the first to see this.
Let's look at the symmetries of the triangle from Jordan's point of view. Instead of placing shaded dots in the corners of the triangle, I will place the symbols
a, b, c
, corresponding to the roots of the general cubic. It then becomes obvious that each symmetry of the triangle also permutes these symbols. For example, the rotation
U
sends
abc
to
cab.
The six symmetries of the triangle correspond naturally to the six permutations of the roots
a
,
b
,
c
. Moreover, the product of two symmetries corresponds to the product of the corresponding permutations. But rotations
and reflections in the plane are linear transformationsâthey preserve straight lines. So we have reinterpreted the permutation groupâ
represented
itâas a group of linear transformations, or equivalently as a group of matrices. This idea was to have profound consequences for both mathematics and physics.
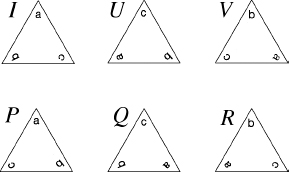
How symmetries of the equilateral triangle correspond to permutations.
THE MEDIOCRE ENGINEER AND THE TRANSCENDENT PROFESSOR
N
o longer was symmetry some vague impression of regularity or an artistic feeling of elegance and beauty. It was a clear mathematical concept with a rigorous logical definition. You could calculate with symmetries and prove theorems about them. A new subject was born:
group theory.
Humanity's quest for symmetry had reached a turning point. The admission fee for this advance was a willingness to think more conceptually. The concept of a group was an abstract one, several stages removed from the traditional raw materials of numbers and geometrical shapes.
Groups had already proved their worth by resolving an age-old conundrum, the solvability of the quintic. It soon became clear that the same circle of ideas disposed of several other age-old problems. You didn't always need group theory as such, but you needed to think like Abel, Galois, and their successors. And even when you thought you weren't using groups, they often lurked in the background.

Among the unsolved problems the Greek geometers bequeathed to posterity, three had become notorious: the problems of trisecting the angle, duplicating the cube, and squaring the circle. Even today, trisection and circle-squaring attract the attention of numerous amateurs, who seem not to have grasped that when mathematicians use the word “impossible,” they mean it. Duplicating the cube seems not to have the same allure.
These three are often referred to as the “three problems of antiquity,” but this phrase exaggerates their importance. It makes them appear to be on a par with major historical puzzles such as Fermat's Last Theorem, which went unanswered for more than 350 years. But this puzzle was explicitly recognized as an unsolved problem, and it is possible to identify the precise point in the mathematical literature where it was first posed. All mathematicians were aware not just of the problem but the presumed answerâand who had first asked the question.
The Greek problems are not like that. You won't find them listed in Euclid as unsolved problems that need attention. They exist mainly by default: they are obvious extensions of positive results, but for some reason Euclid avoided them. Why? Because no one knew how to solve them. Did it occur to the Greeks that they might not
have
solutions? If so, no one made much fuss. It undoubtedly occurred to people like Archimedes that no straightedge-and-compass solutions existed, because he developed alternative techniques, but there is no evidence that Archimedes considered the issue of constructibility important in its own right.
Later it became important. The lack of solutions to these problems pointed to major gaps in humanity's understanding of geometry and algebra; they gained currency as “folklore” problems, known to the professionals through a kind of cultural osmosis. By the time they were solved, they had taken on an aura of historical and mathematical significance. Their solutions were seen as major breakthroughsâespecially squaring the circle. And in all three cases, the answer was the same: “It can't be done.” Not with the traditional tools of straightedge and compass.
This may seem rather negative. In most walks of life, people seek to answer questions or overcome difficulties by whatever means comes to hand. If a tall building cannot be constructed from bricks and mortar, engineers use steel frames and reinforced concrete. No one gains fame by proving that bricks are not up to the job.
Mathematics is not quite like that. The limitations of the tools are often just as important as what they can accomplish. The importance of a mathematical question often depends not on the answer as such, but on why the answer is correct. So it was for the three problems of antiquity.

The scourge of trisectors everywhere was born in Paris in 1814, and his name was Pierre Laurent Wantzel. His father was first an army officer and
later professor of applied mathematics at the Ãcole Speciale du Commerce. Pierre was precocious; Adhémard Jean Claude Barré de Saint-Venant, who knew Wantzel, wrote that the boy showed “a marvelous aptitude for mathematics, a subject about which he read with extreme interest. He soon surpassed even his master, who sent for the young Wantzel, at age nine, when he encountered a difficult surveying problem.”
In 1828, Pierre successfully applied to enter the Collège Charlemagne. He won first prize in both French and Latin in 1831, and he came in first in both the entrance examination for the Ãcole Polytechnique and that for the science section of what is now the Ãcole Normale, which no one had ever done before. He was interested in just about everythingâmathematics, music, philosophy, historyâand he liked nothing better than a good, hard-fought debate.
In 1834, he turned his mind to engineering, attending the Ãcole des Ponts et Chaussées. But soon he was confessing to his friends that he would be “but a mediocre engineer,” decided that he really wanted to teach mathematics, and took a leave of absence. The switch worked: he became a lecturer in analysis at the Ãcole Polytechnique in 1838, and by 1841 he was also a professor of applied mechanics at his old engineering school. Saint-Venant tells us that Pierre “usually worked during the evening, not going to bed until late in the night, then reading, and got but a few hours of agitated sleep, alternatively abusing coffee and opium, taking his meals, until his marriage, at odd and irregular hours.” The marriage was to his former Latin coach's daughter.
Wantzel studied the works of Ruffini, Abel, Galois, and Gauss, developing a strong interest in the theory of equations. In 1837 his paper “On the means of ascertaining whether a geometric problem can be solved with straightedge and compass” appeared in Liouville's
Journal de Mathématiques Pures et Appliquées.
It took up the story of constructibility where Gauss had left off. He died in 1848 at the age of 33âprobably as a result of overwork from an excess of teaching and administrative duties.

On the questions of trisection and duplicating the cube, Wantzel's impossibility proofs resemble Gauss's epic work on regular polygons, but are much easier. I'll start with the duplication of the cube, where the issues are very transparent. Does there exist a straightedge-and-compass construction for a line of length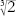 ?
?
Gauss's analysis of regular polygons is based on the idea that any geometric construction boils down to solving a series of quadratic equations. He pretty much takes this for granted, because it follows algebraically from properties of lines and circles. Some reasonably easy algebra implies that the “minimum polynomial” of any constructible quantityâthe simplest equation that it satisfiesâhas degree equal to a power of two. That equation may be linear, quadratic, quartic, octic (degree 8), of degree 16, 32, 64, . . . but whatever the degree is, it is a power of two.
