Why Beauty is Truth (49 page)

In 1926, he was contacted by a crystallographer at the Kaiser Wilhelm Institute who wanted a research assistant. The duties would combine both of Wigner's interests, in a chemical context. The project had a huge influence on Wigner's career, and thus on the course of nuclear physics, because it introduced him to group theory—the mathematics of symmetry. The first major application of group theory to physics had been the classification of all 230 possible crystal structures. Wigner wrote, “I received a letter from a crystallographer who wanted to find out why the atoms occupy positions in the crystal lattices which correspond to symmetry axes. He also told me that this had to do with group theory and that I should read a book on group theory and then work it out and tell him.”

Perhaps no less dismayed than his son by Jen
's foray into the tanning trade, Antal Wigner agreed to allow the research assistantship. Jen
started by reading a few of Heisenberg's papers on quantum theory, and developed a theoretical method to calculate the spectrum of an atom with three electrons. But he also realized that his methods would prove extraordinarily complicated for more electrons than three. At this point, he turned for advice to his old acquaintance von Neumann, who suggested he read about group representation theory. This area of mathematics was heavily laden with the algebraic concepts and techniques of the time, notably matrix algebra. But thanks to his studies in crystallography and his familiarity with a leading algebra textbook of the period—Heinrich Weber's
Lehrbuch der Algebra
—matrices posed no problem for Wigner.

Von Neumann's advice proved sound. If an atom possesses some number of electrons, then since all electrons are identical, the atom does not “know” which electron is which. In other words, the equations describing the radiation emitted by that atom must be symmetric under all permutations of those electrons. Using group theory, Wigner developed a theory of the spectrum of atoms with any number of electrons.

To that point, his work had taken place within the traditional realm of classical physics. But quantum theory was where the excitement was. Now he embarked on his life's masterwork, the application of group representation theory to quantum mechanics.

Ironically, he did so despite, not because of, his new job. David Hilbert, the elder statesman of German mathematics, had developed a keen interest in the mathematical principles behind quantum theory and required the services of a research assistant. In 1927, Wigner went to Göttingen to join Hilbert's research group. His ostensible role was to provide physical insight to inform Hilbert's vast mathematical expertise.

It didn't quite work out as planned. The two met only five times in the course of a year. Hilbert was old, tired, and increasingly reclusive. So Wigner went back to Berlin, gave lectures on quantum mechanics, and continued to put together his most famous book:
Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra.

He had been partly anticipated by Hermann Weyl, who had also written a book about groups in quantum theory. But Weyl's main focus was on foundational issues, whereas Wigner wanted to solve specific physical problems. Weyl was after beauty, Wigner was seeking truth.

We can understand Wigner's approach to group theory in a simple, classical context, the vibrations of a drum. Musical drums are usually circular, but in principle they can be any shape. When you hit a drum with a stick, the skin vibrates and makes a noise. Different shapes of drum produce different sounds. The range of frequencies a drum can produce, called its
spectrum
, depends in a complex manner on the drum's shape. If the drum is symmetrical, we might expect the symmetry to show up in the spectrum. It does, but in a subtle way.

Imagine a rectangular drum—you don't see these often outside of mathematics departments. The typical patterns of vibration for such a drum divide it into a number of smaller rectangles, for example:

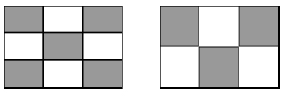
Two patterns of vibration of a rectangular drum.

Here we see two different vibrational patterns with two different frequencies. The pictures are snapshots of the patterns, taken at one instant. The dark regions are displaced downward, the white ones upward.

The symmetries of the drum have implications for the patterns, because any symmetry transformation of the drum can be applied to a possible pattern of vibration to produce another possible pattern of vibration. So the patterns come in symmetrically related sets. However, individual patterns need not have the same symmetries as the drum. For instance, a rectangle is symmetric under rotation through 180°. If we apply this symmetry transformation to the two patterns above, they become:

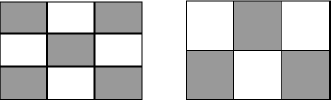
The same two patterns after rotating the drum through 180°.

The left-hand pattern is unchanged, so it shares the rotational symmetry of the drum. But the right-hand pattern has swapped dark regions for light. This effect is called s
pontaneous symmetry-breaking
, and it is very common in physical systems: it occurs when a symmetric system has less-symmetric states. The left-hand pattern does not break symmetry, but the right-hand one does. Let's focus on the right-hand pattern and see what effect its broken symmetry has.

Although the pattern and its rotation are different, they both vibrate at the same frequency, because rotation is a symmetry of the drum and hence of the equations that describe its vibrations. So the spectrum of the drum contains this particular frequency “twice.” It may seem difficult to detect that effect experimentally, but if you make small changes in the drum that destroy its rotational symmetry—say by making a small indentation along one edge—then the two frequencies drift slightly apart, and you can spot that there are two of them, very close together. This would not have happened if the frequency had occurred only once for the symmetric drum.

Wigner realized that the same effect arises with symmetric molecules, atoms, and atomic nuclei. The sounds made by the drum become vibrations of the molecules, and the spectrum of sounds is replaced by the spectrum of emitted or absorbed light. In the quantum world, the spectrum is created by transitions between different energy states, and the atom emits photons whose energy—hence frequency, thanks to Planck—
corresponds to that difference. Now the spectrum can be detected using a spectroscope. Again, some of the frequencies—observed as spectral lines—may be double (or multiple) because of the symmetry of the molecule, atom, or nucleus.

How can we detect this multiplicity? We can't make an indentation in the molecule, as we did for the drum. But we can place the molecule in a magnetic field. This also destroys the underlying symmetry and splits the spectral lines. Now you can use group theory—more strictly, group representation theory—to calculate the frequencies and how they split.

Representation theory is one of the most beautiful and powerful mathematical theories, but it is also technically demanding and full of hidden pitfalls. Wigner turned it into a high art. Others struggled to follow his lead.

By 1930, Wigner had secured a part-time post in America, at the Institute for Advanced Study, and he shuttled between Princeton and Berlin. In 1933, the Nazis passed laws forbidding Jews to hold university jobs, so Wigner moved permanently to the United States—mainly at Princeton, where he anglicized his name to Eugene Paul. His sister Margit joined him in Princeton. There she met Dirac, who was visiting, and in 1937 the two were married, to everyone's amazement.

Margit's marriage worked out fine, but Eugene's job did not. In 1936, Wigner wrote, “Princeton dismissed me. They never explained why. I could not help feeling angry.” Actually, Wigner resigned, apparently because he was not advancing sufficiently quickly. Presumably he believed that Princeton's refusal to promote him had effectively forced him to resign, so he felt as though he had been fired.

He quickly found a new job at the University of Wisconsin, took US citizenship, and met a physics student named Amelia Frank. They married, but Amelia had cancer and died within a year.