Why Beauty is Truth (30 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

At this point, mathematicians faced an unusual dilemma. They had made a distinction between algebraic numbers and transcendental ones, and they believed it would be important. But they still did not know whether any transcendental numbers existed. In practical terms, the supposed distinction might be meaningless.
It took until 1844 to prove the existence of transcendentals. The breakthrough was made by Liouville, who had previously salvaged Galois's work from the academic rubbish heap. Now Liouville managed to invent a transcendental number. It looked like this:
0.110001000000000000000001000. . .,
where longer and longer sequences of 0's are separated by isolated 1's. The important point is that the lengths of the blocks of zeros have to increase very rapidly.
Numbers of this kind are “almost” rational. There exist unusually good rational approximationsâbasically thanks to those blocks of zeros. The long block above, for instance, with 17 consecutive zeros, implies that what comes before itâ0.110001âis a much better approximation
to Liouville's number than you might expect of a random decimal fraction. And 0.110001, like any finite decimal, is rational: it is equal to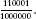 Instead of being accurate to six decimal places, it is accurate to 23 decimal places. The next nonzero digit is a 1 in the 24th place.
Instead of being accurate to six decimal places, it is accurate to 23 decimal places. The next nonzero digit is a 1 in the 24th place.
Liouville had realized that algebraic numbers, other than rational ones, are always rather
badly
approximated by rationals. Not only are such numbers irrational; to get a good rational approximation you have to use very big numbers in any fraction that gets close. So Liouville deliberately defined his number to have extraordinarily good rational approximations, much too good for it to be algebraic. Therefore it had to be transcendental.
The only criticism we can direct against this clever idea is that Liouville's number is very artificial. It has no evident connection with anything else in mathematics. It is plucked from thin air for the sole reason that it can be very well approximated by rationals. No one would care about it at all save for that one remarkable feature: it is provably transcendental. So now mathematicians knew that transcendentals did exist.
Whether
interesting
transcendentals existed was another matter, but at least the theory of transcendental numbers had some content. Now the task was to provide interesting content. Above all, is Ï transcendental? If it were, that would knock the old squaring-the-circle problem on the head. All constructible numbers are algebraic, so no transcendental is constructible. If Ï is transcendental, it is impossible to square the circle.

The number Ï is justly famous because of its connections with circles and spheres. Still, mathematics contains other remarkable numbers, and the most importantâprobably even more important than Ïâis known as
e
. Its numerical value is approximately 2.71828, and like Ï it is irrational. This number arose in 1618, in the early days of logarithms; it determines the correct interest rate if compound interest is applied over ever-shorter intervals. It was called
b
in a letter Leibniz wrote to Huygens in 1690. The symbol
e
was introduced by Euler in 1727, and it appeared in print in his
Mechanics
of 1736.
By using complex numbers, Euler discovered a remarkable relation between
e
and Ï, often considered the most beautiful formula in mathematics. He proved that
e
iÏ
= â1. (This formula does have an intuitive explanation, but it involves differential equations.) After Liouville's dis
covery, the next step to the proof that Ï is transcendental took a further 29 years, and it applied to the number
e
. In 1873 the French mathematician Charles Hermite proved that
e
is transcendental. Hermite's career has remarkable parallels with that of Galoisâhe went to Louis-le-Grand, was taught by Richard, tried to prove that the quintic is unsolvable, and wanted to study at the Ãcole Polytechnique. But unlike Galois he got inâby the skin of his teeth.
One of Hermite's students, the famous mathematician Henri Poincaré, observed that Hermite's mind worked in strange ways: “To call Hermite a logician! Nothing can appear to me more contrary to the truth. Methods always seemed to be born in his mind in some mysterious way.” This originality served Hermite well in his proof that
e
is transcendental. The proof was an elaborate generalization of Lambert's proof that Ï is irrational. It also employed calculus; it evaluated an integral in two ways; and if
e
were algebraic, those two answers would be different: one equal to zero, one nonzero. The difficult step was to find the right integral to compute.
The actual proof occupies about two printed pages. But what a wonderful two pages! You could search for a lifetime and not discover the right choice of integral.
The number
e
is at least a “natural” object of mathematical study. It crops up all over mathematics and is absolutely vital to complex analysis and the theory of differential equations. Although Hermite had not cracked the problem of Ï, he had at least improved on Liouville's rather artificial example. Now mathematicians knew that the everyday operations of mathematics could throw up entirely reasonable numbers that turned out to be transcendental. Soon a successor would use Hermite's ideas to prove that one of those numbers was Ï.

Carl Louis Ferdinand von Lindemann was born in 1852, the son of a language teacher, Ferdinand Lindemann, and the headmaster's daughter, Emilie Crusius. Ferdinand changed jobs, becoming the director of a gasworks.
Like many students in late-nineteenth-century Germany, Lindemann Jr. moved from one university to anotherâGöttingen, Erlangen, Munich. At Erlangen he took a PhD on non-Euclidean geometry under the supervision of Felix Klein. He traveled abroad, to Oxford and Cambridge, and then to Paris, where he met Hermite. On obtaining his habilitation in
1879, he obtained a professorship at the University of Freiburg. Four years later he moved to the University of Königsberg, where he met and married Elizabeth Küssner, a teacher's daughter who worked as an actress. Ten years after that, he became a full professor at the University of Munich.
In 1882, halfway between his trip to Paris and his appointment to Königsberg, Lindemann figured out how to extend Hermite's method to prove the transcendence of Ï, and became famous. Some historians believe that Lindemann just got luckyâthat he was a bit of a hack who blundered across the right extension of Hermite's magnificent idea. But as the golfer Gary Player once remarked, “The better I play, the luckier I get.” So, most likely, was it with Lindemann. If
anyone
could get lucky, why didn't Hermite?
Later, Lindemann turned to mathematical physics, investigating the electron. His most famous research student was David Hilbert.
Lindemann's proof of the transcendence of Ï used the method pioneered by Lambert and developed by Hermite: write down a suitable integral, calculate it two ways, and show that if Ï is algebraic the answers disagree. The integral was very closely related to the one used by Hermite, but even more complicated. The connection between
e
and Ï, in fact, was the beautiful relationship discovered by Euler. If Ï were algebraic, then
e
would have to have some new and surprising propertiesâanalogous to, but differing from, being algebraic. The core of Lindemann's proof is about
e
, not about Ï.
With Lindemann's proof, this chapter of mathematics reached its first truly significant conclusion. That it was impossible to square the circle was barely a sideshow. Much more important was that mathematicians knew why. Now they could go on to develop the theory of transcendental numbers, which today is an activeâand fiendishly difficultâarea of research. Even the most obvious and plausible conjectures about transcendental numbers remain mostly unanswered.

Armed with the insights of Abel and Galois, we can revisit the problem of constructing regular polygons. For which numbers
n
is the regular
n
-gon constructible with straightedge and compass? The answer is extraordinary.
In the
Disquisitiones Arithmeticae
, Gauss stated necessary and sufficient conditions on the integer
n
, but he proved only their sufficiency. He
claimed to possess a proof that these same conditions are also necessary, butâlike much of his workâhe never published it. Gauss had actually done the hard part, and it was Wantzel who filled in the missing details in his 1837 paper.
To motivate Gauss's answer, we briefly review the regular 17-gon. What is it about the number 17 that makes the regular 17-sided polygon constructible? Why is this not the case for numbers like 11 or 13?
Notice that all three numbers here are primes. It is easy to show that if a regular
n
-gon is constructible, then so is the regular
p
-gon for every prime
p
dividing
n.
Just take every
n
/
p
th corner. For example, taking every third vertex of a regular 15-gon yields a regular 5-gon. So it makes sense to think about prime numbers of sides, and to use the results for the primes to work your way toward a complete solution.
The number 17 is prime, so that's a good start. Gauss's analysis, reformulated in more modern terms, is based on the fact that the solutions of the equation
x
17
â 1 = 0 form the vertices of a regular 17-gon in the complex plane. There is one obvious root,
x
= 1. The other 16 are the roots of a polynomial of degree 16, which can be shown to be
x
16
+
x
15
+
x
14
+. . .
x
2
+
x
+ 1 = 0. The 17-gon is constructed by solving a series of quadratic equations, and it turns out that this is possible because 16 is a power of 2. It equals 2
4
.
