Nonplussed! (16 page)

To cause the first move to leave the value of the polynomial unchanged we require that
x
^n+
1
+x
^n+
2
= x
ⁿ
, which means
x + x
²
= 1 and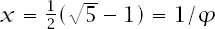
and the Golden Ratio appears once more.

So, if we make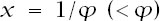
we are assured that the requirements are satisfied and further that, for this value of
x
,
x + x
²
= 1.

Whatever our starting configuration below the dividing line, there will be a finite number of squares occupied. This means that any starting position evaluated at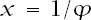
would be less than that of the ‘infinite’ polynomial generated by the occupation of every one of the infinite number of squares. We can find an expression for this by adding the terms in ‘vertical darts’, as illustrated in
figure 6.5
.

Adding terms in this way results in the expression

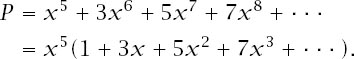
The series in the brackets is a standard one (sometimes known as an arithmetic–geometric series) and is summed in the same way as a standard geometric series

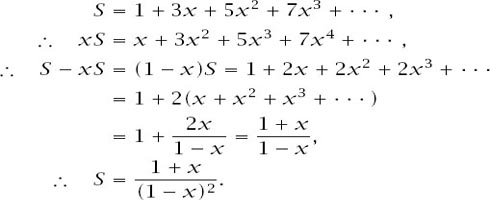
Multiplying by the
x
⁵
term gives the final expression as

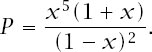
Since our chosen value for
x
satisfies
x + x
²
= x(
1
+ x) =
1, it must be that 1
+ x =
1
/x
and also 1
- x = x
²
. Therefore,

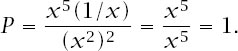
This means that the value of any starting position must be strictly less than 1 and since each move reduces or maintains the value of the position, the value of a position can never reach 1. It is impossible, therefore, to reach level 5.

The proof can be seen to fail with the lower levels. For example, with level 4 we finish with the product

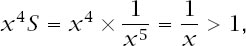
leaving room for a reduction of the position to exactly 1.

THE TOSS OF A NEEDLE

Philosophy is a game with objectives and no rules. Mathematics is a game with rules and no objectives.

Ian Ellis

The
Society for the Diffusion of Useful Knowledge
, founded (mainly by Lord Brougham) in 1828, had the object of publishing information for people who were unable to obtain formal teaching, or who preferred self-education. The celebrated English mathematician and logician Augustus De Morgan was a gifted educator who contributed no less than 712 articles to one of the society’s publications, the
Penny Cyclopaedia
: one of them (published in 1838 and titled
Induction
) detailed (possibly for the first time) a rigorous basis for mathematical induction.

It would appear that De Morgan was contacted by more than his fair share of people whom we might now call mathematical cranks or, to use his own word,
paradoxers
, defined by him in the following way:

A great many individuals, ever since the rise of the mathematical method, have, each for himself, attacked its direct and indirect consequences. I shall call each of these persons a paradoxer, and his system a paradox. I use the word in the
old sense: a paradox is something which is apart from general opinion, either in subject matter, method, or conclusion.

His unwelcome exposure to

squarers of the circle, trisectors of the angle, duplicators of the cube, constructors of perpetual motion, subverters of gravitation, stagnators of the earth, builders of the universe…

inspired the (posthumously published)
Budget of Paradoxes
, a revised and extended collection of letters to another significant publication, the Athenæum journal.

The
Budget
is an eclectic collection of comments, opinions and reviews of ‘paradoxical’ books and articles which De Morgan had accumulated in his own considerable library, partly by purchase at bookstands, partly from books sent to him for review or by the authors themselves. It seems that one James Smith, a successful Liverpool merchant working at the Mersey Dock Board, was the most persistent cause of such aggravation:

Mr. Smith continues to write me long letters, to which he hints that I am to answer. In his last of 31 closely written sides of note paper…

Mr Smith’s conviction was that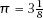
(which he seemed to ‘prove’ by assuming the result and showing that all other possible values then led to a contradiction). The reader may enjoy delving a little deeper into the world of mathematical cranks by reading Woody Dudley’s delightful book of that name.

It is small wonder then that De Morgan picked on probability as a rich seam for the paradoxers to mine, but he recognized it as a seam which contained more than fool’s gold. Again, from the
Budget
we read

The paradoxes of what is called chance, or hazard, might themselves make a small volume. All the world understands that there is a long run, a general average; but a great part of the world is surprised that this general average should be computed and predicted. There are many remarkable cases of verification; and one of them relates to the quadrature of
the circle…. I now come to the way in which such considerations have led to a mode in which mere pitch-and-toss has given a more accurate approach to the quadrature of the circle than has been reached by some of my paradoxers. The method is as follows: Suppose a planked floor of the usual kind, with thin visible seams between the planks. Let there be a thin straight rod, or wire, not so long as the breadth of the plank. This rod, being tossed up at hazard, will either fall quite clear of the seams, or will lay across one seam. Now Buffon, and after him Laplace, proved the following: That in the long run the fraction of the whole number of trials in which a seam is intersected will be the fraction which twice the length of the rod is of the circumference of the circle having the breadth of a plank for its diameter. In 1855 Mr. Ambrose Smith, of Aberdeen, made 3,204 trials with a rod three-fifths of the distance between the planks: there were 1,213 clear intersections, and 11 contacts on which it was difficult to decide. Divide these contacts equally, and we have 1,218 1/2 to 3,204 for the ratio of 6 to 5Pi, presuming that the greatness of the number of trials gives something near to the final average, or result in the long run: this gives Pi=3.1553. If all the 11 contacts had been treated as intersections, the result would have been Pi=3.1412, exceedingly near. A pupil of mine made 600 trials with a rod of the length between the seams, and got Pi=3.137. This method will hardly be believed until it has been repeated so often that ‘there never could have been any doubt about it.’

We will look into this peculiar phenomenon, but first we will mention some related games.

Fairground Games

The study of ‘geometric probability’, where probabilities are determined by comparison of measurements, seems to have had its birth in 1777 (as did the greatest of all mathematicians, Gauss) in the paper, ‘Sur le jeu de franc-carreau’, published by Georges Louis Leclerc, Comte de Buffon. The game of throwing
a small coin (‘
un ecu
’) onto a square grid was a popular pastime and the question of a fair fee to play the game naturally arose; put another way, what is the probability that the coin lands wholly in a square tile (‘
à franc-carreau
’)?

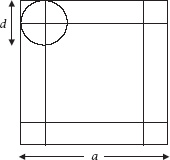
Figure 7.1.
The coin on the square

Buffon correctly argued that the coin would land entirely within a square tile whenever the centre of the coin landed within a smaller square, whose side was equal to the side of a grid square less the diameter of the coin, as we see in
figure 7.1
.

If the grid square is of side
a
and the coin has diameter
d
(which we will suppose is not greater than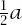
), this means that, if we write this probability as
p
, we have

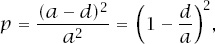
where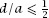
.

For the game to be fair, the expected value of the game must be 0 and so, if it costs 1 unit to play and we are given
w
units if we win,

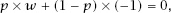
which gives

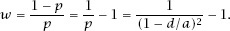
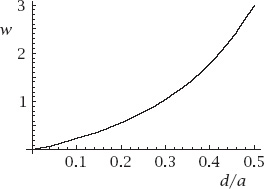
A plot of
w
against
d
/
a
is given in
figure 7.2
.