Nonplussed! (23 page)

Figure 9.6.
The Rowett dice nets.

Table 9.2.
Possibilities when the Rowett dice are thrown twice.

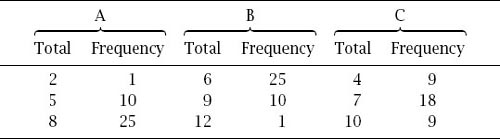
Table 9.3.
The Rowett dice compared again.

To add to the confusion, alter the game to one in which one of the dice is chosen by each player and thrown twice with the winner the person with the higher total.
Table 9.2
gives the three possible totals for each die and the frequency with which each occurs.

Now, if we perform the calculations as before, we arrive at
table 9.3
, which shows the arrows of dominance are reversed. That is, A → C → B → A and this time with probabilities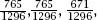
respectively.

Table 9.4.
Effron’s dice compared.

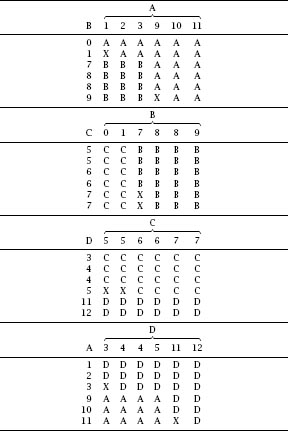
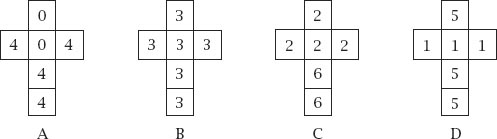
Figure 9.7.
Effron’s dice nets 1.

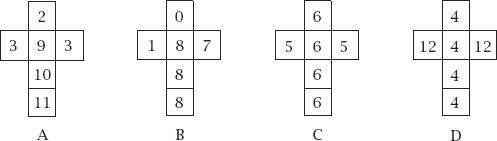
Figure 9.8.
Effron’s dice nets 2.

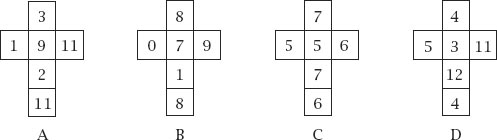
Figure 9.9.
Effron’s dice nets 3.

Effron’s Dice

Bradley Effron, a statistician at Stanford University, extended the idea to four dice, giving the specification for three such sets, as shown in
figures 9.7
–
9.9
. In each case, A → B → C → D → A.

This is a little more subtle since the possibility of draws (rethrows) exists and we will take the trouble to compile the tables, shown as
table 9.4
. In each table, the event of matching numbers is represented by an X.

The ambiguity is exactly the same in all four cases and we can representatively deal with just the first, with A competing with
B. If we write
p
for the probability that A wins, we have

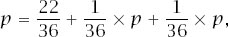
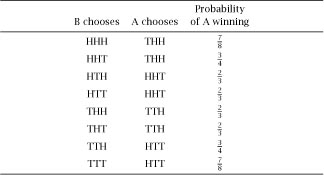
Table 9.5.
Coin-tossing comparisons.

which makes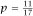
and so A → B with a probability of
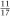and, of course, the probability is the same for the other pairings.

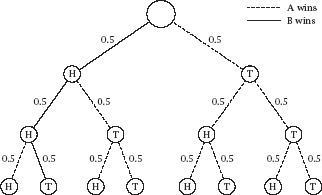
Coin Tossing

The second type of nontransitive effect that we will consider involves the spin of a fair coin. Inevitably, Martin Gardner has considered it, but the author first came across the phenomenon in the Warwick University mathematics magazine
Manifold
, which has long since disappeared. Player A takes a fair coin and repeatedly spins it but before doing so asks player B to choose a sequence of three heads and tails, for example, HTH. Having done so, A chooses his own sequence. The coin is repeatedly spun until one of the two sequences appears: whosoever’s sequence it is, wins. There are only eight possible choices for the triplet and B might reasonably think that somewhere among them there is a best choice, but there isn’t.