Nonplussed! (10 page)
Authors: Julian Havil

Figure 4.4.
A table and its sub-tables
(2) Now suppose that
n
≥ 2 is composite and let
p
be its largest prime factor. If the player has fewer than (1−1
/p)n
hands, then he has no winning strategy.
Write
n = pl
. The argument essentially reduces this case to the previous one. Rather than consider the table cyclically, picture it as
l
copies of a sub-table of
p
sides. For example, if
n =
6 = 2
×
3, we can think of the hexagonal table in
figure 4.4
(a) as the superposition of the two triangular sub-tables in
figure 4.4
(b).
Since the player has fewer than
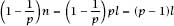
hands at any probe, at least one of the sub-tables will have at least two gaps when the full table is probed, since if each had at
most one gap, there would have to be at least
l×(p-
1
) = (p-
1
)l
hands. Suppose that on a sub-table the two gaps are a distance
j
apart.
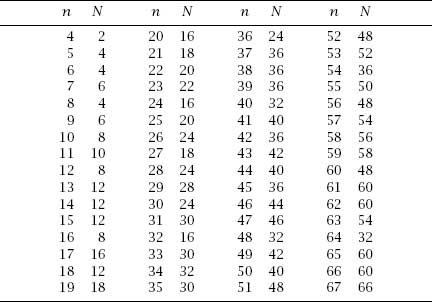
Table 4.1.
Minimum number of hands,
N
, needed for
n
-sided tables.
There must exist a sub-table whose pockets contain glasses of both orientations. Take a walk around it as before in steps of length
j
and, as before, every pocket will be visited before returning to the starting place and this means that there will be two pockets, a distance
j
apart, one of which contains an ‘up’ glass and the other a ‘down’ glass. If the table happens to align itself so that a probe’s sub-table with two gaps is aligned with the sub-table with the glasses of both orientations and with the gaps and the up and down glasses superimposed, the bell cannot ring. This can continue indefinitely, denying any possibility of an assured ringing of the bell.
We should note in passing that (for
n >
2), since
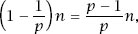
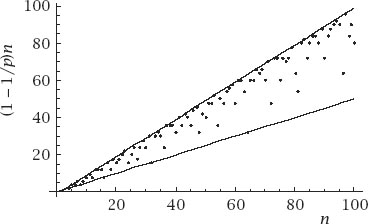
Figure 4.5.
if
p =
2, then
n
must be a power of 2, otherwise
p >
2 and so
p -
1 is even; either way (rather strangely), (1 − 1
/p)n
is even.
We will finish with
table 4.1
, which gives the values of
N = (
1−1
/p)n
for the first few values of
n
, and
figure 4.5
, which graphs the values for
n
up to 100. The trend is clear and reasonable, but regularly upset (most particularly) when
n
is a power of 2, in which case
p
= 2 and
In fact, it is evident that the following bounds exist for
N
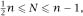
with the lower limit achieved when
N
is a power of 2 and the upper limit when
N
is prime. This is indicated by the lines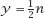 and
and
y = n -
1, which have been added to the plot.

DERANGEMENTS
I think it is said that Gauss had ten different proofs for the law of quadratic reciprocity. Any good theorem should have several proofs, the more the better. For two reasons: usually, different proofs have different strengths and weaknesses, and they generalise in different directions: they are not just repetitions of each other.
Sir Michael Atiyah
We shall look at a famous old problem in three different, enlightening ways and then consider three surprising facts originating from it.
An Old Card Game
The French word for 13,
trieze
, was also the name of a commonly played card game of the eighteenth century. It could be considered as a simple patience (or solitaire) game but in its classic form it was played by several individuals, and commonly for money. We will leave it to the man who is credited with its first analysis to explain matters:
The players draw first for who will have the hand. We suppose that this is Pierre, & that the number of the players
is as such as one would wish. Pierre having an entire deck composed of fifty-two cards shuffled at discretion, draws them one after the other, naming & pronouncing one when he draws the first card, two when he draws the second, three when he draws the third, & thus in sequence up to the thirteenth which is a King. Now if in all this sequence of cards he has drawn none of them according to the rank that he has named them, he pays that which each of the players has wagered in the game, & gives the hand to the one who follows him at the right. But if it happens to him in the sequence of thirteen cards, to draw the card which he names, for example, to draw an ace at the time which he names one, or a two at the time which he names two, or a three at the time which he names three, &c. he takes all that which is in the game, & restarts as before, naming one, next two, &c. It is able to happen that Pierre having won many times, & restarting with one, has not enough cards in his hand in order to go up to thirteen, now he must, when the deck falls short to him, to shuffle the cards, to give to cut, & next to draw from the entire deck the number of cards which is necessary to him in order to continue the game, by commencing with the one where he is stopped in the preceding hand. For example, if drawing the last card from them he has named seven, he must in drawing the first card from the entire deck, after one has cut, to name eight, & next nine, &c. up to thirteen, unless he rather not win, in which case he would restart, naming first one, next two, & the rest as it happens in the explanation. Whence it seems that Pierre is able to make many hands in sequence, & likewise he is able to continue the game indefinitely.
This extract (for which we have relied on the translation by Richard J. Pulskamp) is from the book
Essai d’analyse sur les jeux de hazard
, 2nd edn (1713), by Pierre Renard de Montmort. It is followed by an analysis which, in true mathematical fashion, starts with easier cases, moving to a full solution (with significant contributions from Nicolas Bernoulli). Subsequently other luminaries considered variations of the problem, including De Moivre, Euler, Lambert and Laplace, and we will consider what
is probably its most common modern form with its most common name of
rencontre
(a French word which can be translated as ‘meet by chance’), in which the thirteen card limit is replaced by the whole fifty-two cards of the pack. Since it is the form in which Euler considered the problem we will let him explain it with this extract from the article, Calcul de la probabilité dans le jeu de rencontre, which appears in
Memoires de l’academie des sciences de Berlin
7, 1753 (again we have relied on the translation of Richard J. Pulskamp):
The game of rencontre is a game of chance where two persons, each having an entire deck of cards, draw from it at the same time one card after the other, until it happens that they encounter the same card; and then one of the two persons wins. Now, when such an encounter does not happen at all, then it is the other of the two persons who wins. This posed, one asks the probability that each of these two persons will win.
Whatever the order of the cards in one pack, the other pack will consist of some permutation of those cards and we can look at the game from one of the players’ points of view by considering the chance that no
encounter
occurs, which brings us to a useful definition.
Derangements
A permutation which leaves no element fixed has become known as a
derangement
; put another way, a derangement of
n
objects is a permutation of them without fixed points. The number of derangements of
n
objects is usually written as !
n
, spoken as subfactorial
n
.
Of course, not all permutations are derangements: for example,
{
5,1,2,3,4} is a permutation of
{
1,2,3,4,5} in which no number occupies its original place and so is a derangement,
{
5,2,1,3,4} is not, as the 2 remains fixed.
If we take Montmort’s approach and look at the three simplest cases, we can easily see that the single permutation of
{
1} has no derangements, those of
{
1,2} have the single derangement
{
2,1
}
and those of
{
1,2,3
}
have the two derangements
{
2,3,1
}
and
{
3,1,2
}
; this means that
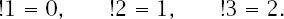
In general, we need to ask the question: Of the !
n
different permutations of
n
distinct objects, how many leave no object in its original place?
The answer to the question will provide a general formula for !
n
and so for
p
n
=
!
n/n
!, the probability that a permutation of
n
objects is a derangement.
Before we begin, we have said that the notation !
n
is standard, but it will be convenient for us to use the alternative
D
n
=
!
n
. The use of !
n
does have something of a visual disadvantage when expressions contain both factorials and subfactorials, as some will in what follows; also, not that it matters to us, the expression !
n
! is ambiguous. For example, !3! might mean (!3)! = 2! = 2 or !(3!
) =
!6 = 265; compare this with the respective equivalents of
D
3
!
=
2 and
D
3
!
=
265.
A First Solution
First, we will find a recurrence relation for
D
n
.
If
{a
1
,
a
2
,
a
3
,
…,a
n
}
is a derangement of
{
1, 2, 3,
…,n}
, it must be that
a
1
≠
1, which leaves
n -
1 possibilities for it; for the sake of illustration we will assume that
a
1
= 2. Now let
d
n
be the number of such derangements, which means that
D
n
= (n -
1
)d
n
. Now there are two possibilities:
(1)
a
2
= 1, which means that the derangement has the form
{
2,1,
a
3
,
a
4
,
a
5
,
…,a
n
}
, where
{a
3
,
a
4
,
a
5
,
…,a
n
}
is a derangement of
{
3,4,5,
…,n}
, and there are exactly
D
n-2
of these;
(2)
a
2
≠
1, with
{a
2
,
a
3
,
a
4
,
…,a
n
}
a derangement of
{
1, 3, 4,
…,n}
; there are
D
n-1
of these.
These combine to mean that
d
n
= D
n-1
+ D
n-2
and therefore
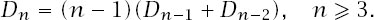
(Incidentally, this means that
D
n
must be divisible by
n -
1.)
Table 5.1.
Numbers of derangements for small sets.
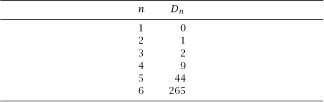
Knowing that
D
1
= 0 and
D
2
= 1, this relation will allow us to generate
D
n
for any
n
and
table 5.1
shows the first few of them.
(Using this result and induction, it is also easy to establish that
D
n
= nD
n-1
+ (-1)
n
.)
We are interested in
p
n
= D
n
/n
!, the probability of a permutation of
n
objects being a derangement, and the recurrence relation that we have just derived allows us to begin to find a general expression for this:
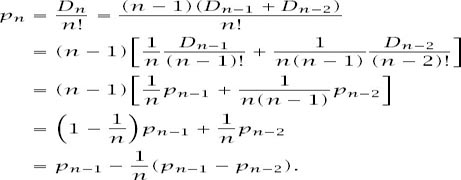
And so,

