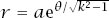Nonplussed! (26 page)
Authors: Julian Havil

We will not pursue his argument fully, partly as we have no wish to delve much into complex numbers here, but the ‘evidently true’ part of the statement seems to rely on two substitutions of variables:
•
X
=
x
- i
y
and
Y
=
x
+ i
y
, which transforms the equation to
Y
2
= λ
X
, a parabola;
•
X
= (
x
+ i
y
)/(
x
- i
y
) and
Y
=
x
+ i
y
, which transforms the equation to
XY
= λ, a rectangular hyperbola.
That it is also an equiangular spiral is shown by recourse to the polar form of complex numbers,
z
=
r
e
i
θ
. The equation may be written in the form
z
2
=
λz
*
, where
z
* is the complex conjugate of
z
, the polar form of which is
z
* =
r
e
−i
θ
. His equation then becomes
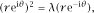
which simplifies to
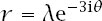
and the equiangular spiral has resurfaced once more!
Now to our central problem.
Our Pursuit Problem
In these earlier examples the pursuer is aware not only of the speed of the pursuer but also the direction in which he is travelling; what happens if we remove this second piece of intelligence? Doing so brings us to our problem:
A smuggler, travelling as fast as possible in a straight line, is being pursued and caught up by a coastguard when a fog-bank engulfs them and each becomes invisible to the other. The smuggler’s boat is too small for electronic detection or to leave an appreciable wake to follow, yet in spite of the coastguard not knowing where the smuggler is or in which direction he is then travelling, he can steer a course that guarantees capture of the smuggler.
One of the crucial words here is
guarantees
. This is not a matter of luck, not a question of probability; the smuggler will be caught with certainty, and with the use of a combination of that Circle of Apollonius and that logarithmic spiral.
The Solution
First we employ the Circle of Apollonius. Writing the speed of the coastguard as
υ
c
and that of the smuggler as
υ
s
and (for convenience)
k
=
υ
c
/
υ
s
> 1, we construct
figure 10.7
in the following way.
Assume that the smuggler enters the fogbank at
P
1
and that the coastguard is then at
S
1
. Define the number
d
by the condition that the distance
S
1
P
1
= (
k
+ 1)
d
and construct the Circle of Apollonius
C
1
of all points
A
so that
AS
1
=
kAP
1
and let it cross
S
1
P
1
at the point
Y
; it is the case, then, that
S
1
Y
=
kd
and
YP
1
=
d
. The captain of the coastguard vessel could aim for any
point on
C
1
and, if he is lucky enough for the pirate to have chosen the appropriate direction, the interception will take place at
Z
, as we saw in the earlier example.
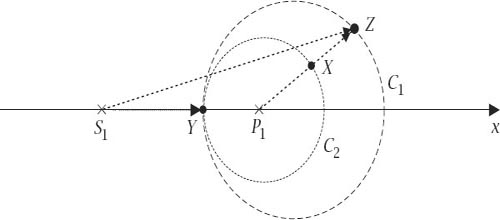
Figure 10.7.
The solution diagram.
Now consider a different coastguard strategy: travel from
S
1
to
Y
(a distance of
kd
) and so be a distance
d
from
P
1
. Since
υ
s
= (1/
k
)
υ
c
, the smuggler will have travelled a distance
d
and therefore be at some point
X
, somewhere on the circle
C
2
, which has centre
P
1
and radius
d
. At this time both the smuggler and the coastguard are distant
d
from
P
1
. The plan now will be for the coastguard to maintain the same distance as the smuggler from
P
1
and for their paths to cross. With
P
1
as the origin and relative to the positive
x
-direction, write the polar equation of the coastguard’s subsequent path as
r
=
r
(
θ
), with
θ
measured anticlockwise from that direction. We will ensure that they both maintain the same distance from
P
1
if we make d
r
/d
t
=
υ
s
. If
s
is the distance the coastguard has travelled from
Y
, then d
s
/d
t
=
υ
c
, which makes
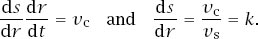
Now we use a standard result of calculus, the detail of which is given in appendix C,
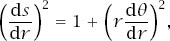
which means that
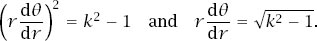
Rewritten as a standard integral, this becomes
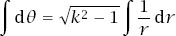
the solution to which is
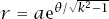
for some constant
a
, and we have the polar equation of the logarithmic spiral.
We also have the condition that
r
=
d
when
θ
=
π
and we can use this to evaluate the constant
a
. The equation