A Player's Guide to Chords and Harmony (41 page)
Read A Player's Guide to Chords and Harmony Online
Authors: Jim Aikin

In practical terms, what this means is that if you play a low A and an E that's an octave and a 5th above it, the fundamental of the E will be at the same frequency as the second overtone of the A. Your ear will be able to perceive this intuitively: The E and the A will sound pleasant together, because there won't be much (if any) beating between them.
EQUAL TEMPERAMENT
Looking at Figure B-I, you might assume that our scale is built using the pitches in the natural harmonic series. This assumption would be about half right and half wrong. In fact, the scale used in European/American music is the result of a set of compromises. The intervals in the scale are derived from the harmonic series, but a bit of fudging has been required to make everything come out right. In order to explain the fudging (and what it means harmonically), we'll have to take a short digression to talk about frequency ratios.
A ratio is a relationship between two numbers. We've already noted, in Chapter One, the fact that any note in the scale has twice the frequency of the note an octave below it. Another way to say this is that the frequency ratio between the two notes is 2:1. (If you're reading aloud, you would read this as "two to one")
A scale comprising no intervals but octaves wouldn't be very interesting. To fill in the octave with other pitches, we need to use other ratios. To build the chromatic scale, our musical ancestors also used the ratios 3:2 and 5:4. These ratios define the intervals of the perfect 5th and major 3rd. (These intervals are discussed in Chapter Two.)
The discussion that follows may seem a bit abstract. The reason it's important is because the actual sound quality of the chords we use today depends in large part on the relative frequencies of the tones in the chord. This is especially true of major triads.
The 3:2 and 5:4 intervals occur naturally in the real world, because they're part of the harmonic series. In Figure B-1, the distance between the A and C# in the treble clef is a ratio of 5:4 (550 divided by 440). No matter what frequency we choose for the fundamental, the frequencies of the fourth and fifth partials will have this ratio, and they'll be a major 3rd apart.
If you have a stringed instrument handy, you can verify this for yourself by playing harmonics. A harmonic is played by touching the string lightly while playing it. The string must be touched at a point that divides its length into equal fractions. If you touch the string at the halfway point, for instance, and then play it, you'll hear a tone an octave above the pitch of the open string. For purposes of discussion, let's suppose that the length of the open string is 24 inches. When you touch it at the halfway point, each half vibrates separately, so in effect you're playing two strings, each of which is 12 inches long. Cutting the length in half doubles the frequency. (If you're technically minded, you'll understand that there is an inverse relationship between string length and frequency.) The ratio of the string lengths is 24:12, which is the same as 2:1.
When you touch the string at a point exactly 1 /3 of the way along its length, it vibrates in three separate segments. The length ratio is 24:8, or 3:1, and the tone produced by the string is an octave and a 5th above the open string. When you touch it at the 1/5 point, it vibrates in five separate segments, producing a 5:1 ratio, which is two octaves and a major 3rd above the open string. Isolating such a high harmonic on a physical string is difficult, but it can be done with bowed instruments.
Without getting into a lot of mathematical detail, we'll merely note that if the string length of the 2:1 (octave) harmonic node is 12 inches, while the string length produced by the 3:1 (octave and a fifth) harmonic node is 8 inches, the ratio of these two string lengths is 12:8, which is the same as 3:2. This is the ratio of the perfect 5th interval.
In the early days, instruments were often tuned so that the pitches of their open strings were in exactly these ratios. But as the black keys were added to the keyboard, and as composers started to use them to produce more complex chords and scales, a vexing difficulty became apparent. Intervals that looked the same size on the keyboard - that encompassed the same number of half-steps - didn't necessarily have the same frequency ratios. Some of them would sound in tune, while others sounded unpleasantly out of tune.
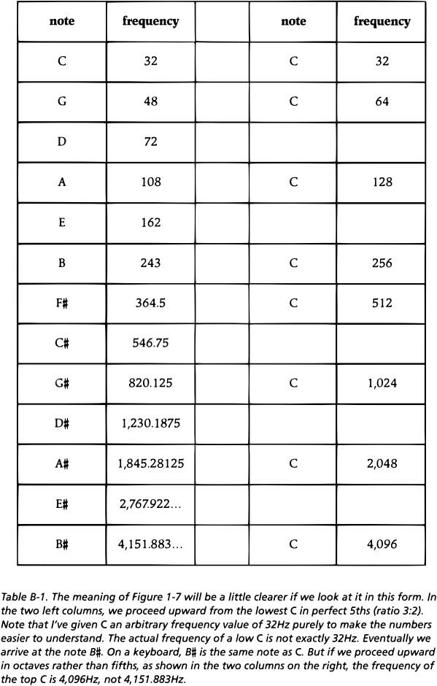
To see why this is the case, let's create a tuning system using nothing but the interval of the perfect 5th. (This is called a Pythagorean tuning, after the semimythical Greek mathematician Pythagoras, whose followers first proposed it.) We'll start with a low note, as shown in Figure B-2 and Table B-1, and "stack" perfect 5ths until we've covered all 12 pitches in the chromatic scale. When we arrive back at B#, which on the keyboard is the same note as C, we find a discrepancy: The pitch of B# is 4,151.88Hz, while the pitch of the C in the same octave is only 4,096Hz. If we play this B# and C at the same time, we'll hear rapid beating, because the distance between them is almost 55Hz.
In order to tune B# to the same frequency as C, it's necessary to make all of the "perfect" 5ths in the scale just slightly narrower than a perfect 3:2 ratio. If we crunch them together in this manner, we'll end up with a scale in which all of the 5ths are slightly out of tune. This is, in fact, the equal-tempered scale that's used today. It's a compromise, but a fairly effective one. The 5th, which is the basis of much of our music, is very close to 3:2, so it doesn't sound at all bad. If anything, the slow beating gives it a warm character.

Figure 8-2. Stacking perfect 5ths (which have a 3:2 frequency ratio) is one way to build a 12-note chromatic scale. To make the numbers easier to read, I've given the frequency of C as exactly 32Hz.
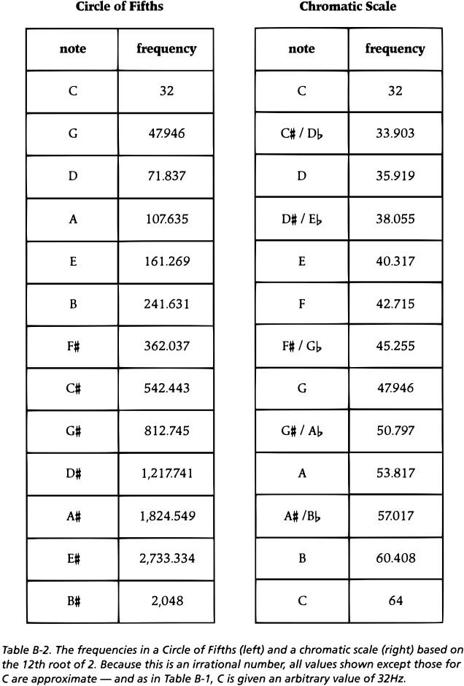
Here's another way to look at the equal-tempered scale: Each half-step has exactly the same frequency ratio as every other half-step. This allows us to play in any key and have the music sound the same. But in order to divide an octave (a 2:1 ratio) into 12 equal steps, for each half-step we have to use the ratio of the twelfth root of 2 to 1. The 12th root of 2 is an irrational number: It's about 1.059463, but not exactly, since an irrational number by definition has an infinite number of digits following the decimal point. If you multiply 1.059463 by itself 12 times, you'll end up with about 1.999999, which is pretty close to 2.
Remember that we said a major 3rd has a frequency ratio of 5:4. If we tune the note C to 32Hz, for example, as in Table B-2, we would expect that the E above this C would have a frequency of exactly 40Hz (because 40:32 is the same ratio as 5:4). Looking at the equal-tempered scale in Table B-2, however, you may notice something odd: The frequency shown for E is not 40Hz but about 40.317Hz. In other words, the major third in the equal-tempered scale is wider than it would be if it were based on an ideal harmonic ratio.
If we tried to build a chromatic scale using 5:4 major thirds, however, we'd get in trouble immediately. Starting with a 32Hz C and moving upward from C through an augmented triad (C-E-G#-C), as shown in Figure B-3, we'd arrive at an octave C (actually another variety of B#) with a frequency of 62.5Hz rather than 64Hz. Thus if we built a scale by stacking 5:4 major thirds, the octave would be noticeably flat. Widening the major 3rd so that stacking three of them gives us a perfect octave produces exactly the same scale as narrowing the perfect 5th so that the B# in the Circle of Fifths is the same as C. Either way, we end up with an equal-tempered chromatic scale in which the half-step ratio is the 12th root of 2.
Because the equal-tempered major 3rd is wider than a 5:4 ratio, you'll hear prominent beats when you play this interval. The beats give the equal-tempered major triad a bright, edgy sound. Since you've been hearing this triad all your life, and may even have been taught that it's good-sounding and "consonant" (a term defined in Chapter Two), you may never notice consciously that it isn't actually very restful. My suspicion, however, is that composers in the 19th and 20th centuries went further and further afield harmonically, exploring more and more exotic chord voicings and chord progressions, in no small part because the equaltempered major triad doesn't sound very good. It doesn't produce a feeling of stability or repose, so composers found themselves avoiding or obscuring it.

Figure B-3. Stacking major 3rds that are based on a perfect 5:4 ratio gives us an octave that's noticeably flat. In an equal-tempered scale, the upper B# is the same note as C, but here it has a frequency of 62.5Hz rather than the 64Hz that would be an octave above the low C.
Interpreting history, especially the history of art, is a chancy business at best. This theory is highly speculative. A more conservative interpretation would be that the restless energy of the 18th and 19th centuries drove composers to develop new forms of harmonic expression, and that the equal-tempered scale was developed precisely in order to allow them this degree of harmonic freedom. In a more stable culture, the equal-tempered scale might never have arisen, because composers wouldn't have needed it.
In any case, because this book talks about how simple chord voicings can be developed into more complex voicings (as happened during this period in history), it would be irresponsible not to put the development of that harmonic language in some sort of context. Since most musicians never have any reason to venture outside the bounds of the 12-note equal-tempered scale, however, there's no particular reason to say any more about it here.
 C:
C:
