A Player's Guide to Chords and Harmony (40 page)
Read A Player's Guide to Chords and Harmony Online
Authors: Jim Aikin

Rests. Since each measure has to have the same total number of beats, special symbols are needed to indicate any beats on which the musician is not supposed to play. These symbols are called rests. Figure A-8 shows what rests look like. Rests can be dotted, just like notes.

Figure A-8. Each note value has a corresponding rest. The rest is the same length as the note. A whole-rest (top) looks a lot like a half-rest (just below it). Here's a mnemonic for remembering which is which: Imagine that the two rests are glued to the lines. The whole-rest needs to have its whole surface covered with glue to keep from falling off, but the half-rest might only be half glued on.
Accidentals. In order to indicate when the black keys on the keyboard are to be played, symbols called accidentals are used. The most important three accidentals for you to know about are the flat (6), the sharp (#), and the natural (q). The flat lowers the pitch of a note by a half-step: Instead of playing the white key indicated in Figure A-2, when you see a flat before the note you should play the black key immediately to the left of the white key. If there isn't a black key im mediately to the left - if the flat occurs before the note C or F - play the white key immediately to the left instead. The sharp raises the pitch of a note by a halfstep, so when you see a sharp before a note you should play the black key immediately to the right of the white key (or, if there isn't a black key immediately to the right, as in the case of E and B, play the white key immediately to the right). These options are summarized in Figure A-9. The natural cancels a flat or sharp, so when you see a natural you should play the white key assigned to that line or space, ignoring any flats or sharps that might previously have been applied to that pitch.
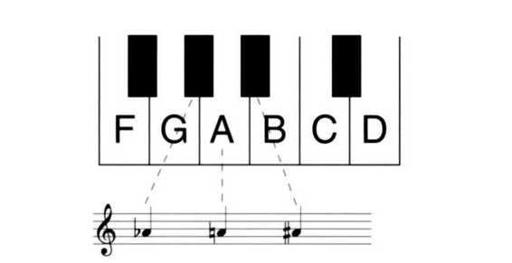
Figure A-9. The flat before the first quarter-note indicates that the black key below the A should be played. The natural cancels a flat or sharp, indicating that the white key should be played. The sharp before the third quarter-note indicates that the black key above the A should be played.
Because of the way the keyboard is laid out, each black key can be indicated on the staff in two different ways. It can be written by putting a note on the line or space corresponding to the next lower white key and placing a sharp before the note to raise the pitch. Or the note can be positioned on the line or space corresponding to the next higher white key, and a flat can be placed before the note to lower the pitch. Two examples are given in Figure A-10. The rules for whether to call a given black key a flat or a sharp are discussed in Chapter One.
Accidentals are used in two ways. First, an accidental can be placed directly before a single note anywhere on the staff. When this is done, the accidental applies to that note and also to any other note on the same line or space that follows the accidental within the same measure - that is, until the next bar line is reached. A bar line cancels this type of accidental. Second, one or more sharps or flats can be placed at the left end of the staff, immediately after the clef, as shown in Figure A-11. The group of accidentals at the left end of the staff is called the key signature. When an accidental appears in the key signature, all of the notes anywhere on the staff that have that letter-name (whether or not they're in the same octave as the accidental) are flatted or sharped.
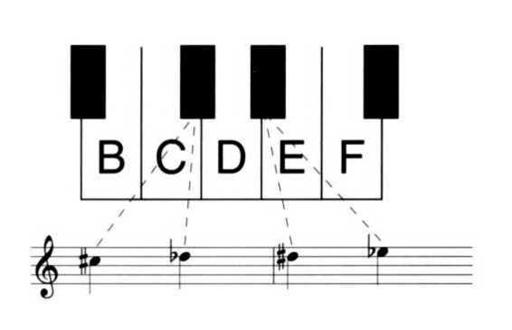
Figure A-10. A black key can be "spelled" using either of two different letter-names. The black key between C and D can be referred to either as a C# or as a D6, for instance. The black key between D and E, meanwhile, can be referred to either as a D# or as an E6.

Figure A-11. The key signature, which appears at the left end of the staff next to the clef, indicates that all notes with the corresponding letter-name are to be played either a halfstep higher (if the key signature shows a sharp) or a half-step lower (if the key signature shows a flat) than the white key that would otherwise be played.
APPENDIX B:
THE HARMONIC SERIES &
EQUAL TEMPERAMENT

 ost music written today, at least in the European/American tradition (which is increasingly dominant around the world), uses a scale consisting of 12 equally spaced pitches. This scale is highly artificial. It was developed in the early 1700s; prior to that time, a number of other tuning systems were in use in European music, and of course in the music of other cultures. In order to explain this scale, we need to take a brief detour to talk, at least briefly, about the harmonic series.
ost music written today, at least in the European/American tradition (which is increasingly dominant around the world), uses a scale consisting of 12 equally spaced pitches. This scale is highly artificial. It was developed in the early 1700s; prior to that time, a number of other tuning systems were in use in European music, and of course in the music of other cultures. In order to explain this scale, we need to take a brief detour to talk, at least briefly, about the harmonic series.
Using a process developed by an 18th-century French mathematician named Jean-Baptiste Fourier (pronounced "four-yay"), any sound can be analyzed as the sum of one or more sine waves, each of which has its own amplitude, frequency, and phase characteristics. What exactly is a sine wave? The term has a mathematical meaning, but don't worry about it. Think of a sine wave as a sort of sonic atom or building block - the simplest possible sound.
In most tones created by musical instruments (except for drums and a few others), the frequencies of the various sine waves have simple mathematical relationships to one another. All of them are whole-number multiples of the lowest frequency in the tone. In the real world of vibrating physical objects, they may not be exact multiples, but the numbers are close enough that we don't need to worry about any discrepancies.
The lowest frequency is called the fundamental. The various sine waves are all called partials or harmonics, and all of the partials above the fundamental are called overtones. So if the fundamental is, for instance, at 110Hz, the tone will contain overtones at 220Hz, 330Hz, 440Hz, and so on, as shown in Figure B-1. Any series of tones that are whole-number multiples of one another is said to be part of the harmonic series, and individual tones within such a series are called harmonics.

Figure B-1. Most tones in nature consist of numerous partials, which vibrate at frequencies that are wholenumber multiples of the lowest partial. The lowest partial is called the fundamental. Shown here is a fundamental frequency of 110Hz (which happens to be an A) and its first five overtones. Note that the overtone series continues upward indefinitely, only the lower overtones are shown.
If you're interested in a little more academic rigor, you might appreciate knowing the following facts:
1. Every sound consists of one or more partials, which are sine waves.
2. If the partials are close to being whole-number multiples of some frequency, then this frequency is called the fundamental, and all of the higher partials are called overtones. The second partial (counting from the bottom) is the first overtone.
3. If the partials are not whole-number multiples of some frequency, the sound is said to be clangorous (meaning that it sounds more or less like a bell) or noisy (meaning random). In the case of noise, the number of partials is technically infinite, because noise is defined as a signal that contains energy at all frequencies.
Unless the overtones are unusually loud (usually they won't be as loud as the fundamental), our ears will identify the frequency of the fundamental as being the frequency of the tone itself. The other partials, rather than being perceived separately, will contribute to the perceived tone color of the tone.
As mentioned in Chapter One, in the section on playing in tune, whenever two tones with different pitches are sounded at once, a third tone called a difference tone can also be perceived. The frequency of the difference tone is the difference (found by subtraction) between the frequencies of the other two tones. Here's the key point: If the partials are harmonically related, as in Figure B-1, the difference tones between partials will also be harmonically related. For instance, if two of the partials above a 100Hz fundamental are at 400Hz and 500Hz, then they create a 100Hz difference tone.
