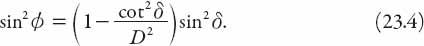X and the City: Modeling Aspects of Urban Life (70 page)

Noting that triangle
OO′R
is a right triangle, it follows from these equations that

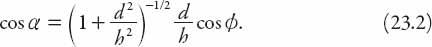
Now we are in a position to express the distance
R
of the scattering drops, relative to the height of the light source (so
R
=
r
/
h
) in terms of the relative distance of the observer,
D
=
d
/
h
, and the angles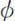
and
δ
after some algebra as

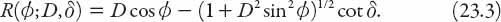
Note both from the equation and the polar plots in
Figure 23.5
that
R
is symmetric about the polar axis,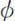
= 0, and that if
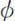= 180°, then
R
= −(
D
+ cot
δ
). Also, if
D
= 0, the plot reduces to a circle of radius
R
= −cot
δ
≈ 1.11).

What exactly do these polar graphs tell us? That’s a good question. They show the distance
R
of the rainbow (or more accurately, that of the corresponding raindrops) in units of
h
along the beam as a function of beam orientation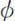
for given values of
D
. This is the distance (also in units of
h
) of the observer from the base of the lighthouse. Simply put, the graphs show the points (in the horizontal plane through
L
) where the observer sees the primary bow. (A similar set of graphs can be drawn for the secondary bow.) To interpret this, note that the observer is on the line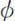
= 0° (the positive
x-
axis) at a distance
D
from the origin at
L
. For the case of
D
= 0.5 the rainbow lies on a slightly squashed circle as the beam rotates; for
D
= 1.11 the rainbow moves along the beam toward
L
and eventually coalesces with the light source when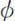
= 180°. The case for
D
> 1.11, (specifically
D
= 2 here) is interesting. The dotted loop represents the position of the rainbow if there were
two beams
180° apart. When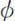
= 146° the rainbow would emerge from
L
and move outward along the “backward” beam until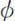
= 180° and then move back toward
L
and continue in the counterclockwise path as shown. When there is only one beam, the rainbow would rapidly approach
L
(and “disappear” for a short time by remaining there for the duration of the now “virtual” loop) before rapidly reemerging from
L
and proceeding in the larger loop.

But where did the angle of 146° come from? It is calculated by setting
R
= 0 in equation (23.3) and solving the resulting expression for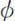
(given a value for
D
), to arrive at