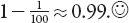X and the City: Modeling Aspects of Urban Life (15 page)

Just for fun, consider SPF 100 (if that exists!).

In this case
, so
or 99% of the harmful radiation is blocked. But you knew that, because

You are walking in a city park (Central Park, for example; but be careful not to trip over the squirrels). Suppose that a jogger passes you. As she does so, at an average speed, say of 8 mph, you wonder if there is an instant when her speed is
exactly
8 mph, or equivalently, 7.5 minutes per mile. Fortunately, you have taken a calculus class, and you recall the mean value theorem, an informal (and imprecise) rendering of which says that for a differentiable function
f
(
t
) on a closed interval there is at least one value of
t
for which the tangent to the graph is parallel to the chord joining its endpoints (why not sketch this?). This means
that if
f
is the distance covered as a function of time
t
, then at some point (or points) on the run her speed will be exactly 8 mph. A formal statement of the theorem can be found in any calculus book when you get home (unless you are carrying it while walking in the park).

The jogger’s name is Lindsay, by the way; by now you’ve seen each other so often that you greet each other as she races past. As she does so yet again, a related question comes to mind: does Lindsay cover any one continuous mile in exactly 7.5 minutes? (Of course, this assumes her run is longer than a mile.) This is by no means obvious, to me at least, and it may not have occurred to Lindsay either.

Suppose that
t
(
x
) is a continuous function representing the time taken to cover
x
miles. We consider this question in two parts. Suppose further that Lindsay runs an integral number (
n
) of miles. If she averages 7.5 min/mi (8 mph), then
t
(
x
) − 7.5
x
= 0 when
x
= 0 and
x
=
n
, i.e.
t
(
n
) = 7.5
n
. If she never covered any continuous mile in 7.5 minutes, then it follows that the new function
T
(
x
) =
t
(
x
+ 1) −
t
(
x
) − 7.5 is continuous and never zero. Suppose that it is always positive; a similar argument applies if it is always negative. Hence for
x
= 0, 1, 2, . . . ,
n
we can write the following sequence of
n
inequalities:
T
(0) > 0;
T
(1) > 0;
T
(2) > 0; . . . 
T
(
n
− 1) > 0. In adding them all a great deal of cancellation occurs and we are left with the inequality
t
(
n
) −
t
(0) > 7.5
n
. This contradicts the original assumption that
t
(
n
) −
t
(0) = 7.5
n
, and so we can say that she
does
cover a continuous mile in exactly 7.5 minutes.

It turns out that this is true for only an integral number of miles, and that seems, frankly, rather strange. We’ll examine this case for a specific function, by redefining
t
(
x
) to be:

where
m
is
not
an integer and
ε
> 0. If
ε
is small enough and
m
is large enough, this will represent an increasing function with small “undulations” about the line 7.5
x
, representing the time to jog at the average speed.
t
(
x
) is an increasing function if
t
′(
x
) > 0, as it must be because it is a time function. Mathematically this will be so if

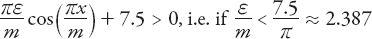
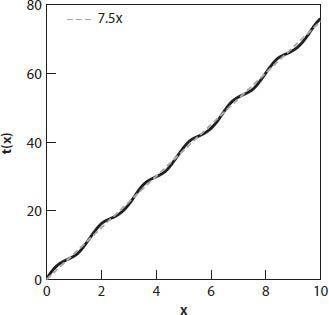
Figure 6.1. Lindsay’s time function
t
(
x
).

for this particular model of the jogging time.
Figure 6.1
shows
t
(
x
) and the mean time function for the case
ε
= 1,
m
= 0.8.

Now it follows that

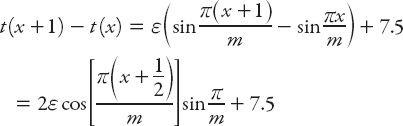
is an increasing function that can
never
be 7.5. Therefore if Lindsay runs so that her time function is given by equation (6.1), she will never run a complete mile in exactly 7.5 minutes.

It seems that it’s almost impossible to find a taxi when it’s raining in the city. Gene Kelly preferred to sing and dance, but, as sometimes happens when I am walking, the heavens open and I am faced with the different options of running fast or walking for shelter. Is it better to walk or
run
in the rain? The
decision to run may seem an obvious one, but depending on several factors discussed below, it is not always that simple. And occasionally I have the foresight to take an umbrell.

What might such factors be? Among them are how fast the rain is falling, and in what direction (i.e., is there wind, and if so, in what direction), how fast I can run or walk, and how far away the shelter is. Let’s ignore the wind and rain direction initially and set up a very basic model. Suppose that you run at
v
m/s. Since 2 mph ≈ 1 m/s, as is easily shown, we can easily convert speeds in mph to MKS units and vice versa. Of course, this is only approximate, but we shall nevertheless use it for simplicity; we do not require precise answers here; after all, we’re in a hurry to get home and dry off!

Suppose the distance to the nearest shelter point is
d
km, and that the rain is falling at a rate of
h
cm/hr (or
h
/3600 cm/s). Clearly, in this simplified case it is better to run than to walk. Here is a standard classification of the rate of precipitation:

• Light rain—when the precipitation rate is < 2.5 mm (≈ 0.1 in) per hour;

• Moderate rain—when the precipitation rate is between 2.5 mm (≈ 0.1 in) and 7.6 mm (0.30 in) to 10 mm (≈ 0.4 in) per hour;

• Heavy rain—when the precipitation rate is between 10 mm (0.4 in.) and 50 millimeters (2.0 in) per hour;

• Violent rain—when the precipitation rate is > 50 mm (2.0 in) per hour.

Now if I run the whole distance
d
m at
v
m/s, the time taken to reach the shelter is
d
/
v
seconds, and in this time the amount
H
of rain that has fallen is given by the expression
H
=
hd
/3600
v
cm. If I run at 6 m/s (about 12 mph), for example, and
d
= 500 m, then for heavy rain (e.g.,
h
= 2 cm/hr),
H
≈ 0.5 cm. This may not seem like a lot, but remember, it is falling on and being absorbed (to some extent at least) by our clothing, unless we are wearing rain gear. The next step in the model is to estimate the human surface area; a common approach is to model ourselves as a rectangular block, but a quicker method is to consider ourselves to be a flat sheet 2 m high and 0.5 m wide. The front and back surface area is 2 m
²
—about right! Over the course of my run for shelter, if all that rain is absorbed, I will have collected an amount 2 × 10
⁴
× 5 × 10
⁻²
= 10
³
, or one liter of rain. That’s a wine bottle of rain that the sky has emptied on you! I prefer the real stuff . . .