Teaching the Common Core Math Standards With Hands-On Activities, Grades 3-5 (44 page)

Procedure

1.
Explain that students will make a line plot of pencil lengths. Explain what a line plot is and offer the example provided in the Background.

2.
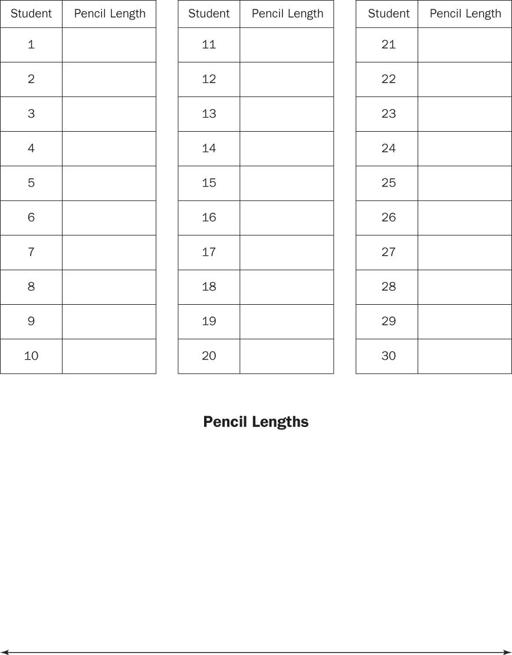
Hand out copies of the reproducible. Explain that it has three columns in which there are spaces for the measurements of 30 students' pencils. There is also a line at the bottom of the sheet that will serve as a line plot that students will complete.

3.
Explain that students are to measure their pencils, using a ruler with a
-inch scale. If necessary, demonstrate how students can find the length of their pencil using the ruler.

• Explain that they must align the end of the pencil with the first tick mark on the ruler.
  
• Note that inches are represented by whole numbers. One tick mark to the right represents
  of an inch. Two tick marks represent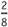
  or
  of an inch. For example, 4 tick marks to the right of 6 is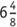
  or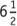
  inches.
  

4.
Call the name of the first student in your grade book. Ask for the length of his or her pencil. Students are to record this length in the space next to Student 1 on the reproducible. You may find it helpful to also record this information on the board.

5.
Continue calling on students, in order according to your grade book, until all students have provided the length of their pencils.

6.
Explain how students can construct their line plot.

• Find the smallest and largest values. In this case, these are the shortest and longest pencil lengths.
  
• Place a small vertical line near the left on the horizontal line at the bottom of the reproducible to represent the smallest pencil length.
  
• Using a ruler and starting with the smallest value, mark the line at
  -inch intervals, stopping at the number that represents the longest pencil length.
  
• Place an X every time a value is given. Label the line plot at 1-inch intervals.
  

7.
Instruct your students to use their completed line plots to write an addition or subtraction problem that can be solved using their line plot. For example: What is the sum of the lengths of the three smallest pencils? What is the difference between the shortest and longest pencils?

8.
Ask for volunteers to read their questions. The other students should solve the problems.

Closure

Discuss students' line plots. Ask how the line plots made it easier to solve the problems that students wrote.

Name _______________________________________ Date
__________

Pencil Lengths

Measurement and Data: 4.MD.5

“Geometric measurement: understand concepts of angle and measure angles.”

5. “Recognize angles as geometric shapes that are formed wherever two rays share a common endpoint, and understand concepts of angle measurement:

a.
“An angle is measured with reference to a circle with its center at the common endpoint of the rays, by considering the fraction of the circular arc between the points where the two rays intersect the circle. An angle that turns through
of a circle is called a ‘one-degree angle,’ and can be used to measure angles.

b.
“An angle that turns through
one-degree angles is said to have an angle measure of
degrees.”