Teaching the Common Core Math Standards With Hands-On Activities, Grades 3-5 (20 page)
Read Teaching the Common Core Math Standards With Hands-On Activities, Grades 3-5 Online
Authors: Judith A. Muschla,Gary Robert Muschla,Erin Muschla-Berry
Tags: #Education, #Teaching Methods & Materials, #Mathematics, #General

3.
Explain that after students have agreed on a design for their garden, they should draw the plan on their graph paper. Suggest a scale of 1 unit on their graph paper equaling 1 foot of the garden. They are to label the lengths of the garden's sides (which must total 50), and then find the area of the garden.
Closure
Have students share their garden designs with other groups. It is likely that the designs will vary. Discuss that although the perimeters of the gardens equal 50, the areas will vary, according to each garden's dimensions. Which garden had the largest area? Which had the smallest? Why?
Areas and Perimeters of Rectangles
Directions: Use square tiles to make the rectangles below. After you make each rectangle, draw it on a separate piece of paper. Then write the lengths of each side and find the perimeter.
1.
Create a rectangle that has an area of 1 square unit.
2.
Create a rectangle that has an area of 2 square units.
3.
Create two rectangles that each has an area of 4 square units.
4.
Create a rectangle that has an area of 5 square units.
5.
Create two rectangles that each has an area of 8 square units.
6.
Create two rectangles that each has an area of 9 square units.
7.
Create two rectangles that each has an area of 10 square units.
8.
Create three rectangles that each has an area of 12 square units.
Perimeters and Areas of Rectangles
Directions: Use square tiles to make the rectangles below. After you make each rectangle, draw it on a separate piece of paper. Then write the lengths of each side and find the area.
1.
Create a rectangle that has a perimeter of 4 units.
2.
Create a rectangle that has a perimeter of 6 units.
3.
Create two rectangles that each has a perimeter of 10 units.
4.
Create three rectangles that each has a perimeter of 12 units.
5.
Create four rectangles that each has a perimeter of 16 units.
Geometry: 3.G.1
“Reason with shapes and their attributes.”
1. “Understand that shapes in different categories (e.g., rhombuses, rectangles, and others) may share attributes (e.g., having four sides), and that the shared attributes can define a larger category (e.g., quadrilaterals). Recognize rhombuses, rectangles, and squares as examples of quadrilaterals, and draw examples of quadrilaterals that do no not belong to any of these subcategories.”
Background
Quadrilaterals (four-sided figures) have three subgroups: trapeziums, which have no parallel sides, parallelograms, which have two pairs of parallel and congruent sides, and trapezoids, which have only one pair of parallel sides.
Parallelograms have two subgroups: rhombuses, which have four congruent sides, and rectangles, which have two pairs of parallel sides, two pairs of congruent sides, and four right angles. A square, having four congruent sides and four right angles, is a rhombus
and
a rectangle.
Parallelogram
serves both as an umbrella term over an entire category (as just described) and as a specific example within that category, namely, a quadrilateral with two pairs of parallel and congruent sides but no right angles. Likewise
rhombus
can refer either to a category of parallelogram that has four congruent sides that might or might not have right angles, or to a specific type of parallelogram with four congruent sides but no right angles.
Activity: Classifying Quadrilaterals
Working in small groups, students will identify which quadrilateral does not belong in a set of three. They are to explain why they believe the figure selected does not belong and then draw a figure that does belong with the other two in the set.
Materials
Scissors; glue sticks; rulers; unlined paper; reproducible, “Which One Does Not Belong?” for each group of students.
Procedure
1.
Explain that quadrilaterals can be classified in many ways: by the number of parallel sides, by the number of congruent sides, by the number of right angles, and by their perimeter and area.
2.
If necessary, review the meanings of the following terms: parallel, congruent, right angle, perimeter, and area. Also, if necessary, provide examples of parallelograms, trapezoids, rhombuses, rectangles, and squares.
3.
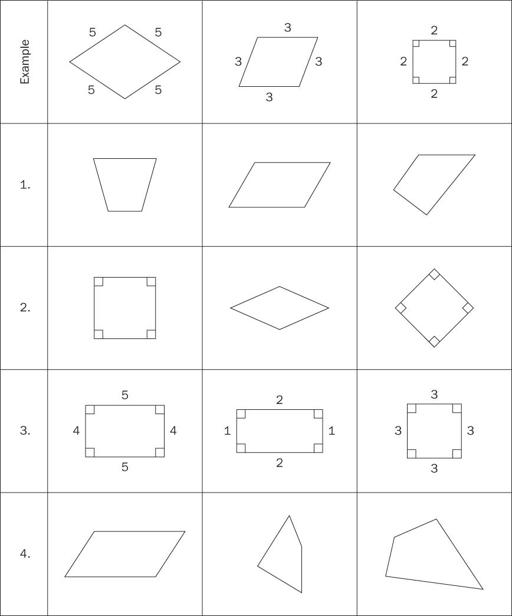
Hand out copies of the reproducible and explain that there are three figures in each row. Two belong in each set of three because they share some of the same features, but one does not. Students are to identify which figure does not belong with the other two and provide a reason why.
4.
Use the first row as an example. Ask your students which figure does not belong with the other two. Students should say the square because it has four right angles.
5.
Explain that once students have identified a figure that does not belong, they should write the number of the row and their reasons why the figure does not belong on a separate sheet of paper. They are to then draw a figure on unlined paper that belongs with the other two, cut the figure out, and glue it over the figure on the reproducible that does not belong. Using the first row as an example again, students should draw a rhombus that is not a square, cut it out, and glue it over the square so that every figure in the row has four congruent sides and no right angles. Instruct your students to follow this procedure for every row on the reproducible.
Closure
Discuss the answers and share your students' correct responses.
Answers: The answer is provided for each problem, followed by placement and description of the sketch.
(1)
Figure two, the parallelogram, does not belong because it has two pairs of parallel sides while the other figures are trapezoids, which have one pair of parallel sides. A trapezoid should be placed over the second figure.
(2)
Figure two, the rhombus, does not belong because it has no right angles while the other figures have four right angles. A square should be placed over the second figure.
(3)
Figure three, the square, does not belong because it has four congruent sides while the other two figures have two pairs of congruent sides. A rectangle that is not a square should be placed over the third figure.
(4)
Figure one, the parallelogram, does not belong because it has two pairs of parallel sides while the other two figures are quadrilaterals that have no parallel sides. A quadrilateral with no parallel sides should be placed over the first figure.
Names ____________________________________ Date
______________
Which One Does Not Belong?
Geometry: 3.G.2
“Reason with shapes and their attributes.”
2. “Partition shapes into parts with equal areas. Express the area of each part as a unit fraction of the whole.”
Background
Geometric figures can be partitioned into parts with equal areas. For example, a 2-by-2 square can be divided into four 1-by-1 squares. The area of each small square is of the area of the 2-by-2 square. The 2-by-2 square can also be partitioned into two 1-by-2 rectangles. The area of each rectangle is
of the area of the 2-by-2 square. The 2-by-2 square can also be partitioned into two 1-by-2 rectangles. The area of each rectangle is of the area of the square.
of the area of the square.
Activity: Decomposing Figures
Working in pairs or groups of three, students will assemble parts of a geometric figure into the original figure. They will represent the area of each part as a unit fraction of the larger figure.
Materials
Scissors; reproducibles, “Parts of Figures, I,” “Parts of Figures, II,” and “Geometric Figures,” for each pair or group of students.
Procedure