Teaching the Common Core Math Standards With Hands-On Activities, Grades 3-5 (42 page)

4.
Encourage students to find information for their posters in their math texts and reference books on measurement. You might also have students conduct research on the Internet.

5.
Suggest that students brainstorm and sketch designs for their posters on a sheet of paper before beginning work on poster paper. Their posters should be attractive and informative.

6.
If time permits, instruct students to start their posters.

Day Two

Provide time for students to complete their posters.

Closure

Have students share their posters with the class. Discuss other examples of things that can be measured by the various units. Display the posters.

Measurement and Data: 4.MD.2

“Solve problems involving measurement and conversion of measurements from a larger unit to a smaller unit.”

2. “Use the four operations to solve word problems involving distances, intervals of time, liquid volumes, masses of objects, and money, including problems involving simple fractions or decimals, and problems that require expressing measurements given in a larger unit in terms of a smaller unit. Represent measurement quantities using diagrams such as number line diagrams that feature a measurement scale.”

Background

Students need to acquire a basic understanding of measurement units. Most math texts include measurement tables, and you should encourage your students to consult the tables whenever necessary.

Activity: Word Problems with Measurement

Working in pairs or groups of three, students will solve word problems involving various measurement units. They are to select one of the problems and represent the measurement quantities in the problem on a number line diagram with a measurement scale.

Materials

Rulers; markers; colored pencils; crayons; graph paper; reproducible, “Measurement Word Problems,” for each pair or group of students.

Procedure

1.
Distribute copies of the reproducible. Explain that it contains five word problems that involve measurement. Students are to solve all five problems.

2.
Explain that after your students solve the problems, they are to select one and represent the measurement quantities on a number line diagram that has a measurement scale. For example, such a diagram might have intervals of inches and half inches, hours and minutes and so on, depending on the problem. Students should create their number line diagram on graph paper with the units on their diagram representing the problem.

3.
Instruct students to write their problem number and the problem's solution under their number line diagram.

Closure

Check students' number line diagrams and discuss the answers to the problems. Note that number lines may vary somewhat, depending on the scales students use. Allow students to share their number lines with others.

Answers

(1)
2.8 miles
(2)
75 minutes, or 1 hour and 15 minutes
(3)
3 cups
(4)
400 grams
(5)
6 quarters, 3 dimes, 1 nickel

Names ____________________________________ Date
______________

Measurement Word Problems

Directions: Solve each problem. Then choose one of the problems and represent it on a number line diagram.

1.
Roseanna walks for exercise. This week she walked a total of 7.6 miles. Last week she walked 4.8 miles. How much farther did she walk this week than last week?

2.
Deon had a lot of homework last night. He finished his spelling homework in 15 minutes. He finished his math in 30 minutes. He finished his science in 20 minutes. And he finished his social studies in 10 minutes. How long did it take him to finish all of his homework? Write your answer in hours and minutes.

3.
Paulo likes his grandmother's fruit juice punch. His grandmother's special recipe calls for
cup of pineapple juice for every quart of punch. Paulo wants to make 1 gallon of punch. How many cups of pineapple juice will he need?

4.
For her science project, Clarice knew that the total mass of 5 solid, equal-sized cubes was 2 kilograms. What was the mass in grams of each cube?

5.
The lunch at Alexandra's school costs $1.85. Alexandra paid for lunch with 10 coins that totaled $1.85. What coins did she have?

Measurement and Data: 4.MD.3

“Solve problems involving measurement and conversion of measurements from a larger unit to a smaller unit.”

3. “Apply the area and perimeter formulas for rectangles in real world and mathematical problems.”

Background

Perimeter and area are two topics that students encounter frequently in math. Perimeter is the distance around a closed plane figure. Area is the number of square units required to cover a surface.

The formula for finding the perimeter of a rectangle is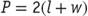
or
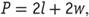where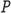
stands for perimeter,
stands for the length of a side of the rectangle, and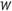
stands for its width. Perimeter is measured in linear units. If students know the perimeter of a rectangle, and they know the length of one side, they can find the length of an adjacent side by multiplying the length of the known side by 2, subtracting the product from the perimeter, and dividing the difference by 2. Understanding that opposite sides of a rectangle are congruent, students will now know the lengths of all the sides.

The formula for finding the area of a rectangle is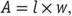
where
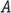stands for the area,
stands for the length of a side, and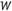
stands for the width. Area is measured in square units. If students understand the formula, and they know the area of a rectangle and the measure of one side, they may divide the area by the measure of the side they know to find the measure of the unknown side.