Nonplussed! (8 page)
Authors: Julian Havil

The next step is to invoke the arithmetic geometric mean inequality, which states that, for any
r
positive numbers,
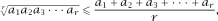
with equality only when all numbers are equal.
With
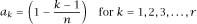
we then have that
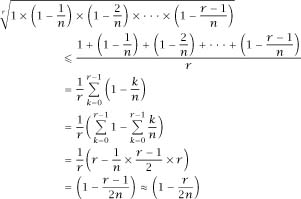
and so,
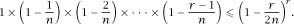
Next we invoke the inequality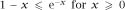 to get
to get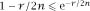 and this means that
and this means that
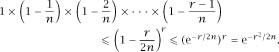
Finding the smallest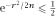 will then give us an upper bound on the smallest
will then give us an upper bound on the smallest
r
such that
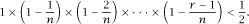
If we consider the ‘equation’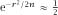 and take natural logs of both sides, we have that
and take natural logs of both sides, we have that
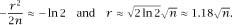
So, for a group of a ‘large’ size
n
we need a sample of at most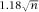 to have an even chance of two of them matching and we can quantify the surprise in the Birthday Paradox by stating that the minimum number required to fulfil the requirements is of the order
to have an even chance of two of them matching and we can quantify the surprise in the Birthday Paradox by stating that the minimum number required to fulfil the requirements is of the order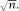 With all of this hand-waving approximation around it is comforting to check that the formula for
With all of this hand-waving approximation around it is comforting to check that the formula for
n =
365 gives the very accurate estimate 22.54.
Halmos continued by saying that
The reasoning is based on important tools that all students of mathematics should have ready access to. The birthday problem used to be a splendid illustration of the advantages of pure thought over mechanical manipulation; the inequalities can be obtained in a minute or two, whereas the multiplications would take much longer, and be much more subject to error, whether the instrument is a pencil or an old-fashioned desk computer. What calculators do not yield is understanding, or mathematical facility, or a solid basis for more advanced, generalized theories.
