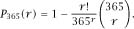Nonplussed! (6 page)

and the use of Pythagoras’s Theorem once again gives the third side of that triangle to be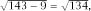
making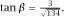

In summary, Leybourn’s instructions reduce to

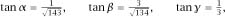
and our inequality requires that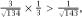
or that 143 > 134, which indeed it is! (Using the same analysis, his lower limit of 5 inches requires that 5159 > 4934.)

With the mystery of the uphill roller explained we will leave the scholarship of Mr Leybourn with part of Samuel Pepys’s diary entry of 18 August 1662:

Mr. Deane of Woolwich came to me, and he and I rid into Waltham Forest, and there we saw many trees of the King’s a-hewing; and he showed me the whole mystery of off square wherein the King is abused in the timber that he buys, which I shall with much pleasure be able to correct.

One of Leybourn’s publications had explained the fraudulent practice of
off square
cutting to the understanding of Mr Deane, an official at Woolwich.

THE BIRTHDAY PARADOX

I’m sixty years of age. That’s 16 Celsius.

George Carlin

The Basic Problem

Perhaps one of the most well-known examples of a counterintuitive phenomenon concerns the likelihood of two individuals in a gathering sharing the same birthday. If we ignore leap years, then, with a gathering of 366 people, we are assured of at least one repetition of a birthday (a simple application of the subtly powerful Pigeon Hole Principle). That observation is clear enough. What is considerably more perplexing is the size of the group which would result in a 50:50 chance of such a repetition; intuition has commonly argued that, since we halve the probability, we should need about half the number of people, around 183. And intuition is much misguided.

Not the Problem

In part, the counterintuitive nature of the result stems from a common misconception of its statement. It is not that, among
r
people, at least one person has the same birthday as oneself, although this is easily calculated.

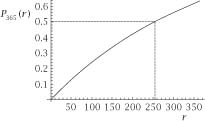
Figure 3.1.
The same birthday as oneself

In an
n
-day year, the probability that a single person will miss the birthday in question is
(n-
1
)/n
and so, assuming independence, the probability that all
r
of them will do so is
((n-
1
)/n)
^r
, which means that the probability of at least one match is

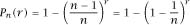
and so, for a standard year,

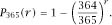
It is clear that, as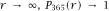
and
figure 3.1
shows enough of the plot of
P
₃₆₅
(r)
for the value 0.5 to be exceeded and at a value of
r
somewhere above 250. To find the exact value of
r
, we must solve
P
₃₆₅
(r) =
0.5, which means finding
r
so that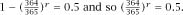
This makes

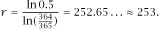
The correct interpretation of the statement of the problem has us not asking that a particular birthday be matched, but that there exist two birthdays that match. A linear increase in
r
results in a combinatorial increase in the possible number of matches, by which we mean that as
r
increases by 1 the number
of possible matches obviously increases by
r
itself. Symbolically,

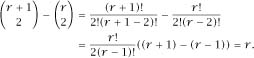
So, for example, increasing
r
from 22 to 23 increases the number of possible matches from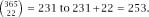
It is this significant rate of increase of possible successes that underlies the solution to the problem.

This deals with the common misconception; now we will move to the real thing.

The Standard Solution

The usual analysis for a year of
n
days and a random collection of
r
people again uses the standard observation that the probability of at least two people having the same birthday is one minus the probability of everybody having different birthdays. That said, the first person’s birthday can be chosen in
n
out of the
n
possibilities and, with this one day used up, the second person’s birthday can then be chosen in
(n -
1
)
ways, etc. Continuing the argument for all
r
we arrive at the expression for the new
P
_n
(r)
, the probability that at least two people have the same birthday, as shown below:

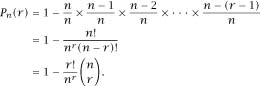
This means that, for a year of 365 days,