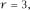Nonplussed! (4 page)

The remaining cubic equation 8
p
³
− 4
p
²
− 2
p -
1 = 0 has the single real root,

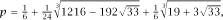
which evaluates to
p
= 0.919 643 ….

Again, for any
p >
0.919 6 …, we will have
P
(0,0
) > P(
40,30), with the paradox once again established.

In conclusion, two equal players who are good enough to win the point on their serve just over 90% of the time are better off at the game’s start than they are when the score is either 30–15 or 40–30 in their favour.

THE UPHILL ROLLER

Mechanics is the paradise of the mathematical sciences because by means of it one comes to the fruits of mathematics.

Leonardo da Vinci

An Advertisement for a Book

The Proceedings of the Old Bailey
dated 18 April 1694 chronicles a busy day devoted to handing down justice, in which 29 death sentences were passed as well as numerous orders for brandings; there would have been 30 death sentences had not one lady successfully ‘pleaded her belly’ (that is, proved that she was pregnant). The business part of the document ends with a list of the 29 unfortunates and continues to another list; this time of advertisements (rather strange to the modern mind), which begins with the following paragraph:

THE Ladies Dictionary: Being a pleasant Entertainment for the Fair Sex; Work never attempted before in English. The Design of this Work is universal, and concerns no less than the whole Sex of Men in some regard, but of Women so perfectly and neatly, that ’twill be serviceable to them in all their Concerns of Business, Life, Houses, Conversations.

Tempting though it is to delve into the details of what suggests itself as a bestselling book, we move to the second advertisement.

Pleasure with Profit: Consisting of Recreations of divers kinds, viz. Numerical, Geometrical, Mathematical, Astronomical, Arithmetical, Cryptographical, Magnetical, Authentical, Chymical, and Historical. Published to Recreate Ingenious Spirit, and to induce them to make further scrutiny how these (and the like) Sublime Sciences. And to divert them from following such Vices, to which Youth (in this Age) are so much inclin’d. By William Leybourn, Philomathes.

Presumably, those who were tried at the assizes had been given insuffcient access to the work and we will touch on only a small part of it ourselves, to be precise, pages 12 and 13.

William Leybourn (1626–1719) (alias Oliver Wallingby) was in his time a distinguished land and quantity surveyor (although he began his working life as a printer). Such was his prestige, he was frequently employed to survey the estates of gentlemen, and he helped to survey the remnants of London after the great fire of 1666. Also, he was a prolific and eclectic author. In 1649 he published (in collaboration with one Vincent Wing)
Urania Practica
, the first book in English devoted to astronomy. After this came
The Compleat Surveyor
, which first appeared in 1653 and ran to five editions, and is regarded as a classic of its kind. His 1667 work,
The Art of Numbering by Speaking Rods: Vulgarly Termed Napier’s Bones
, was significant in bringing them further into the public eye.

In 1694 he had published the recreational volume
Pleasure with Profit
, the opening page of which is shown in
figure 2.1
.

We can readily agree with the following sentiment expressed in the book:

But leaving those of the Body, I shall proceed to such Recreations as adorn the Mind; of which those of the Mathematicks are inferior to none.

And having done so we can then concentrate on a delightful mechanical puzzle described in the book and attributed to one ‘J.P.’, which has become known as the Uphill Roller.

Figures 2.2
and
2.3
show pages 12 and 13 of the book, which detail the construction of a double cone and two inclined rails along which the cone can roll –
uphill
. His final paragraph explains the paradox, pointing out that the important issue is that, even though the cone does ascend the slope, its centre of mass will descend if the measurements are just right, which ensures that, although one’s senses might be confounded, the law of gravity is not.

An Explanation

Before we examine Leybourn’s explanation, we will look at the matter through modern eyes, using elementary trigonometry to study it.
Figures 2.4
,
2.5
and
2.6
establish the notation that we need and parametrize the configuration in terms of three angles:
α
, the angle of inclination of the sloping rails;
ß
, the semi-angle between the rails, measured horizontally at floor level; the semi-angle at an apex of the double cone. Write
a
and
b
as the heights of the lower and upper ends of the rails and
r
as the radius of the double cone. An
x/y
coordinate system is then set up as shown in
figure 2.4
.

With the coordinate system in place, we can find the equation of the path of the centre of mass of the cone as it rolls up the slope. From
figures 2.5
and
2.6
we have

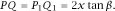
From
figure 2.6
we have

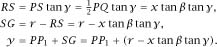
From
figures 2.4
and
2.6
we have

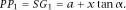
Therefore,

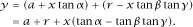
The path of the centre of mass of the cone is, then, the straight line

which has gradient tan
α
− tan
ß
tan
γ
and for the motion to be possible this gradient has to be negative, which means that the defining condition for the paradox to exist is that

Of course, to appreciate the paradox properly, a physical model is needed and the reader is strongly encouraged to make one (or to get someone else to). The author’s model (made by his long-term friend, Brian Caswell) has

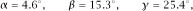
from which it is plain that the inequality just holds.

Leybourn’s Version

Now that we have a clear criterion to use, we can look more closely at Leybourn’s instructions. If we take the diameter of his double cone to be the upper limit of 6 inches and realize that 1 yard is 36 inches, his description translates in our terms to: