Nonplussed! (2 page)
Authors: Julian Havil

If we move from theoretical intelligence levels to real-world matters of the state of health of individuals, we approach the medical concept of
stage migration
and a realistic example of the Will Rogers phenomenon. In medical stage migration, improved detection of illness leads to the fast reclassification of people from those who are healthy to those who are unhealthy. When they are reclassified as not healthy, the average lifespan of those who remain classified as healthy increases, as does that of those who are classified as unhealthy some of whose health has been poor for longer. In short, the phenomenon could cause an imaginary improvement in survival rates between two different groups. Recent examples of this have been recorded (for example) in the detection of prostate cancer (I. M. Thompson, E. Canby-Hagino and M. Scott Lucia (2005), ‘Stage migration and grade inflation in prostate cancer: Will Rogers meets Garrison Keillor’,
Journal of the National Cancer Institute
97:1236–37) and breast cancer (W. A. Woodward et al. (2003), ‘Changes in the 2003 American Joint Committee on cancer staging for breast cancer dramatically affect stage-specific survival’,
Journal of Clinical Oncology
21:3244–48).
Winning on the Serve
Finally, we revert to lighter matters of tennis scoring and look at a situation in which an anomaly in the scoring system can, in theory, be exposed.
The scoring system in lawn tennis is arcane and based on the positions of the hands of a clock. For any particular game it is as follows.
If a player wins his first point, the score is called 15 for that player; on winning his second point, the score is called
30 for that player; on winning his third point, the score is called 40 for that player, and the fourth point won by a player causes the player to win, unless both players have won three points, in which case the score is called deuce; and the next point won by a player is scored ‘advantage’ for that player. If the same player wins the next point, he wins the game; if the other player wins the next point the score is again called deuce. This continues until a player wins the two points immediately following the score at deuce, when that player wins.
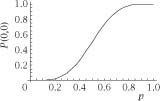
The great tennis players of the past and present might be surprised to learn that, with this scoring system, a
high quality tennis player serving at 40–30 or 30–15 to an equal opponent has less chance of winning the game than at its start.
We will quantify the players being evenly matched by assigning a fixed probability
p
of either of them winning a point as the server (and
q
= 1 −
p
of losing it); for a high quality player,
p
will be close to 1. The notation
P(a,b
) will be used to mean the probability of the server winning the game when he has
a
points and the receiver
b
points; we need to calculate
P
(40,30) and
P
(30,15) and compare each of these with
P
(0,0), which we will see will take some doing!
First, notice that the position at ‘advantage’ is the same as that at (40,30), which means that the situation at deuce, when divided into winning or losing the next point, is given by
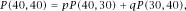
also, using the same logic, we have
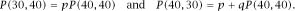
If we put these equations together, we get
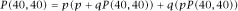
and so
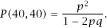
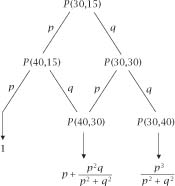
Figure 1.1.
Finding
P
(30,15).
Using the identity 1 − 2
pq = (p + q
)
2
− 2
pq = p
2
+ q
2
we have the more symmetric form for the situation at deuce,
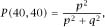
and this makes
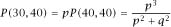
and the first of the expressions in which we have interest is then
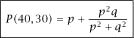
Now we will find the expression for
P
(30,15), which takes a bit more work, made easier by the use of a tree diagram which divides up the possible routes to success and ends with known probabilities, as shown in
figure 1.1
.
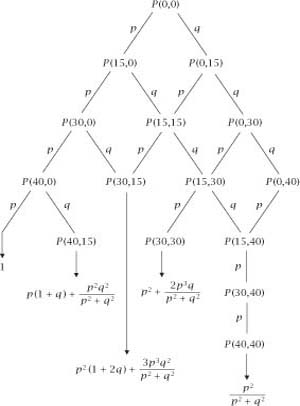
Figure 1.2.
Finding
P
(0,0)
Every descending route is counted to give