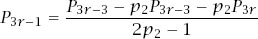Nonplussed! (28 page)
Authors: Julian Havil

but as we approach an infinite resource our probability of losing must approach 0, which means that
Q
= 0 and so
P
= 1. In this case,
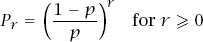
and we conclude that
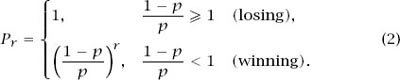
Of course, the inequalities for
p
simplify to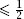 and
and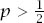 and this accords with our intuitive idea that if the game is fair
and this accords with our intuitive idea that if the game is fair
or biased against us, eventually we will probably lose all of our fortune. As we mentioned before, even a fair game is a losing game if we have no chance of exhausting the opponent’s fortune.
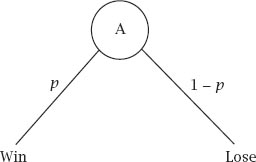
Figure 11.2.
Game A tree diagram.
The Parrondo Setup
This analysis is repeated three times to expose the Parrondo paradox: there will be a game A and another game B, both of which are losing. We will then combine them, to result in a multiple game C, which will prove to be winning.
Game A
This is simply the game we have already described. Think of it as tossing a biased coin and getting a winning head with a fixed probability
p
or a losing tail with probability 1 −
p
. The winning and losing conditions are then represented by the same diagram as before, which is repeated in shortened form in
figure 11.2
. The solution is provided by equation (2) on page 118:
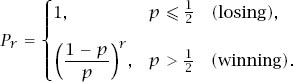
This is more complicated, with the chance of winning on any play of it dependent on the size of the capital at the time. To be exact, if the capital happens to be a multiple of 3, we win with
probability
p
1
; otherwise, we win with probability
p
2
, summed up in
figure 11.3
.
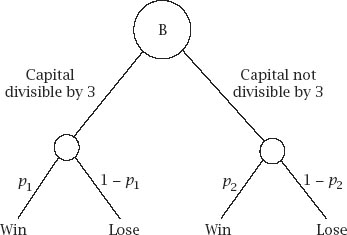
Figure 11.3.
Game B tree diagram.
Since any positive integer must be one of {3
r
, 3
r
+ 1, 3
r
+ 2}, we must consider three recurrence relations, the first generated by the left branch of the diagram and the remainder by its right side.
With
P
r
defined as before we then have
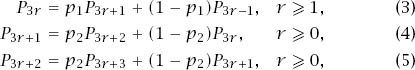
together with the condition
p
0
= 1.
Again, we want an explicit formula for
P
r
in terms of
r
and we work towards this by first finding a formula for
p
3
r
.
The algebra is devious and we start by writing equations (4) and (5) as
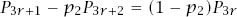
and
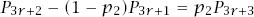
and so think of them as two equations in the two unknowns
p
3
r
+1
and
P
3
r
+2
.
These have the solutions (after some standard but messy algebra)
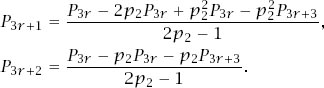
Rewriting
P
3
r
+2
with
r
− 1 replacing
r
then gives