For the Love of Physics (10 page)
Read For the Love of Physics Online
Authors: Walter Lewin
Tags: #Biography & Autobiography, #Science & Technology, #Science, #General, #Physics, #Astrophysics, #Essays

The whole idea of changing weight is so fascinating that I really wanted to be able to demonstrate this phenomenon—even weightlessness—in
class. What if I climbed up on a table, standing on a bathroom scale that was tied very securely to my feet? I thought then maybe I could somehow show my students—by rigging up a special camera—that for the half second or so that I was in free fall the bathroom scale would indicate zero. I might recommend that you try this yourself, but don’t bother; trust me, I tried it many times and only broke many scales. The problem is that the scales you can buy commercially don’t react nearly fast enough, since there is inertia in their springs. One of Newton’s laws bedeviling another! If you could jump off a thirty-story building, you would probably have enough time (you would have about 4.5 seconds) to see the effect, but of course there would be other problems with that experiment.
So rather than breaking scales or jumping off buildings, here’s something you can try in your backyard to experience weightlessness, if you have a picnic table and good knees. I do this from the lab table in front of my classroom. Climb up on the table and hold a gallon or half-gallon jug of water in your outstretched hands, just cradling it lightly on top of them, not holding the sides of the jug. It has to be just resting on your hands. Now jump off the table, and while you are in the air you will see the jug start floating above your hands. If you can get a friend to make a digital video of you taking the jump, and play it back in slow motion, you will very clearly see the jug of water start to float. Why? Because as you accelerate downward the force with which you have been pushing up on the jug, to keep it in your hands, has become zero. The jug will now be accelerated at 9.8 meters per second per second, just as you are. You and the jug are both in free fall.
But how does all of this explain why your scale goes berserk when you lift yourself up on your toes? As you push yourself upward you accelerate upward, and the force of the scale pushing on you increases. So you weigh more for that brief time. But then, at the top of your toes, you decelerate to come to a halt, and that means that your weight goes down. Then, when you let your heels down, the entire process is reversed, and you have just demonstrated how, without changing your mass at all, you can make yourself weigh more or less for fractions of a second.
The Law of Universal Gravitation: Newton and the Apple
People commonly refer to Newton’s three laws, but, in fact, he formulated four. We’ve all heard the story of Newton observing an apple falling from a tree one day in his orchard. One of Newton’s early biographers claimed that Newton himself told the story. “It was occasion’d by the fall of an apple,” wrote Newton’s friend William Stukeley, quoting a conversation he had with Newton, “as he sat in contemplative mood. Why should that apple always descend perpendicularly to the ground, thought he to himself.”
*
But many remain unconvinced that the story is true. After all, Newton only told Stukeley the story a year before he died, and he made no mention of it any other place in his voluminous writings.
Still, what is unquestionably true is that Newton was the first to realize that the same force that causes an apple to fall from a tree governs the motion of the Moon, the Earth, and the Sun—indeed, of all the objects in the universe. That was an extraordinary insight, but once again, he didn’t stop there. He realized that every object in the universe attracts every other object—and he came up with a formula for calculating just how strong the attraction is, known as his universal law of gravitation. This law states that the force of gravitational attraction between two objects is directly proportional to the product of the masses of the objects and inversely proportional to the square of the distance between them.
So, in other words, to use a purely hypothetical example, which I stress has no relation to reality, if Earth and Jupiter were orbiting the Sun at the same distance, then because Jupiter is about 318 times more massive than Earth the gravitational force between the Sun and Jupiter would be about 318 times greater than that between the Sun and Earth. And if Jupiter and Earth were the same mass, but Jupiter were
in its actual orbit, which is about five times farther from the Sun than the Earth’s orbit, then because the gravitational force is inversely proportional to the square of the distance, it would be twenty-five times greater between the Sun and Earth than between the Sun and Jupiter.
In Newton’s famous
Philosophiæ Naturalis Principia Mathematica
published in 1687—which we now call the
Principia
—he did not use an equation to introduce the law of universal gravitation, but that’s the way we express it most often in physics today:
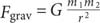
Here,
F
grav
is the force of gravitational attraction between an object of mass
m
1
and one of mass
m
2
, and
r
is the distance between them; the
2
means “squared.” What is
G
? That’s what’s called the gravitational constant. Newton knew, of course, that such a constant exists, but it is not mentioned in his
Principia.
From the many measurements that have since been done, we now know that the most accurate value for
G
is 6.67428 ± 0.00067 × 10
–11
.
*
We physicists also do believe that it’s the same throughout the universe, as Newton conjectured.
The impact of Newton’s laws was gigantic and cannot be overestimated; his
Principia
is among the most important works of science ever written. His laws changed all of physics and astronomy. His laws made it possible to calculate the mass of the Sun and planets. The way it’s done is immensely beautiful. If you know the orbital period of any planet (say, Jupiter or the Earth) and you know its distance to the Sun, you can calculate the mass of the Sun. Doesn’t this sound like magic? We can carry this one step further; if you know the orbital period of one of Jupiter’s bright moons (discovered by Galileo in 1609) and you know the distance between Jupiter and that moon, you can calculate the mass of Jupiter. Therefore, if you know the orbital period of the Moon around the Earth (it’s 27.32 days) and you know the mean distance between the Earth
and the Moon (it’s about 239,000 miles) then you can calculate to a high degree of accuracy the mass of the Earth. I show you how this works in
appendix 2
. If you can handle some math you may enjoy it!
But Newton’s laws reach far beyond our solar system. They dictate and explain the motion of stars, binary stars (
chapter 13
), star clusters, galaxies, and even clusters of galaxies, and Newton’s laws deserve credit for the twentieth-century discovery of what we call dark matter. I will tell you more about this later. His laws are beautiful—breathtakingly simple and incredibly powerful at the same time. They explain so much, and the range of phenomena they clarify is mind-boggling.
By bringing together the physics of motion, of interactions between objects, and of planetary movements, Newton brought a new kind of order to astronomical measurements, showing how what had been a jumble of confusing observations made through the centuries were all interconnected. Others had had glimmers of his insights, but they hadn’t been able to put them together as he did.
Galileo, who died the year before Newton was born, had come up with an early version of Newton’s first law and could describe the motion of many objects mathematically. He also discovered that all objects will fall from a given height at the same speed (in the absence of air drag). He couldn’t, though, explain
why
it was true. Johannes Kepler had worked out the fundamentals of
how
planetary orbits worked, but he had no clue
why.
Newton explained the why. And, as we’ve seen, the answers, and many of the conclusions they lead to, are not in the slightest bit intuitive.
The forces of motion are endlessly fascinating to me. Gravity is always with us; it pervades the universe. And the astounding thing about it—well, one astounding thing—is that it acts at a distance. Have you ever really stopped to consider that our planet stays in orbit, that we are all alive because of the attractive force between two objects 93 million miles apart?
Pendulums in Motion
Even though gravity is a pervasive force in our lives, there are many ways in which the effects it has on our world confound us. I use a pendulum demonstration to surprise students with just how counterintuitively gravity operates. Here’s how it works.
Many of you may think that if you swing on a playground swing next to someone who is much lighter than you are, e.g., a toddler, you’ll go much slower than that person. But that is not the case. It may therefore come as a surprise to you that the amount of time it takes to complete one swing of a pendulum, which we call the period of the pendulum, is not affected by the weight hanging from the pendulum (we call this weight the bob). Note that here I’m talking about what’s called a simple pendulum, which means that it meets two conditions. First, the weight of the bob must be so much larger than the weight of the string that the weight of the string can be ignored. Second, the size of the bob needs to be small enough that we can treat it as if it were just a point, which has zero size.
*
It’s easy to make a simple pendulum at home: attach an apple to the end of a lightweight string that is at least four times longer than the size of the apple.
Using Newton’s laws of motion, I derive in class an equation for calculating the period of a simple pendulum, and then I put the equation to the test. To do that I have to make the assumption that the angle over which the pendulum swings is small. Let me be more precise about what I mean by that. When you look at your homemade pendulum as it swings back and forth, from right to left and from left to right, you will see that most of the time the pendulum is moving, either to the left or to the right. However, there are two times during a complete swing that the pendulum stands still, after which it reverses direction. When
this happens the angle between the string and the vertical has reached a maximum value, which we call the amplitude of the pendulum. If air drag (friction) can be ignored, that maximum angle when the pendulum comes to a halt at the far left is the same as when the pendulum comes to a halt at the far right. The equation that I derive is only valid for small angles (small amplitudes). We call such a derivation in physics a small-angle approximation. Students always ask me, “How small is small?” One student is even very specific; she asks, “Is an amplitude of five degrees small? Is the equation still valid for an amplitude of ten degrees or is ten degrees not small?” Of course, those are excellent questions, and I suggest that we will bring this to a test in class.
The equation that I derive is quite simple and very elegant, though it may look a little daunting to those who haven’t been doing any math lately: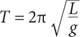
T
is the period of the pendulum (in seconds),
L
is the length of the string (in meters), π is 3.14, and
g
is the gravitational acceleration (9.8 meters per second per second). So the right part of the equation reads two π multiplied by the square root of the length of the string divided by the gravitational acceleration. I won’t go into the details here of why this is the correct equation (you can follow the derivation that I do in my recorded lectures if you want to; the website link is on page 54).
I am giving the equation here so that you can appreciate just how precisely my demonstrations confirm it. The equation predicts that a pendulum 1 meter long has a period of about 2 seconds. I measure the time it takes a pendulum, with a string that long, to complete ten oscillations, and that comes to about 20 seconds. Dividing by 10, we get 2 seconds for the period. Then I go to a pendulum with a string that is four times shorter. The equation predicts that the period should be twice as short. So I make the string 25 centimeters long, and indeed it takes about 10 seconds for ten oscillations. So that is all very reassuring.
