For the Love of Physics (6 page)
Read For the Love of Physics Online
Authors: Walter Lewin
Tags: #Biography & Autobiography, #Science & Technology, #Science, #General, #Physics, #Astrophysics, #Essays

I will admit that I may be a bit biased here, since my PhD research consisted of measuring different kinds of nuclear decay to a high degree of accuracy, and that my contributions in the early years of X-ray astronomy came from my measurements of high-energy X-rays from tens of
thousands of light-years away. But there simply is no physics without measurements. And just as important, there are no meaningful measurements without their uncertainties.
You count on reasonable amounts of uncertainty all the time, without realizing it. When your bank reports how much money you have in your account, you expect an uncertainty of less than half a penny. When you buy a piece of clothing online, you expect its fit not to vary more than a very small fraction of a size. A pair of size 34 pants that varies just 3 percent changes a full inch in waist size; it could end up a 35 and hang on your hips, or a 33 and make you wonder how you gained all that weight.
It’s also vital that measurements are expressed in the right units. Take the case of an eleven-year-long mission costing $125 million—the Mars Climate Orbiter—which came to a catastrophic conclusion because of a confusion in units. One engineering team used metric units while another used English ones, and as a result in September 1999 the spacecraft entered the Martian atmosphere instead of reaching a stable orbit.
In this book I use metric units most of the time because most scientists use them. From time to time, however, I’ll use English units—inches, feet, miles, and pounds—when it seems appropriate for a U.S. audience. For temperature, I’ll use the Celsius or Kelvin (Celsius plus 273.15) scales but sometimes Fahrenheit, even though no physicist works in degrees Fahrenheit.
My appreciation of the crucial role of measurements in physics is one reason I’m skeptical of theories that can’t be verified by means of measurements. Take string theory, or its souped-up cousin superstring theory, the latest effort of theoreticians to come up with a “theory of everything.” Theoretical physicists, and there are some brilliant ones doing string theory, have yet to come up with a single experiment, a single prediction that could test any of string theory’s propositions. Nothing in string theory can be experimentally verified—at least so far. This means that string theory has no predictive power, which is why some physicists, such as Sheldon Glashow at Harvard, question whether it’s even physics at all.
However, string theory has some brilliant and eloquent proponents. Brian Greene is one, and his book and PBS program
The Elegant Universe
(I’m interviewed briefly on it) are charming and beautiful. Edward Witten’s M-theory, which unified five different string theories and posits that there are eleven dimensions of space, of which we lower-order beings see only three, is pretty wild stuff and is intriguing to contemplate.
But when theory gets way out there, I am reminded of my grandmother, my mother’s mother, a very great lady who had some wonderful sayings and habits that showed her to be quite an intuitive scientist. She used to tell me, for instance, that you are shorter when standing up than when lying down. I love to teach my students about this. On the first day of class I announce to them that in honor of my grandmother, I’m going to bring this outlandish notion to a test. They, of course, are completely bewildered. I can almost see them thinking, “Shorter standing up than lying down? Impossible!”
Their disbelief is understandable. Certainly if there is any difference in length between lying down and standing up it must be quite small. After all, if it was one foot, you’d know it, wouldn’t you? You’d get out of bed in the morning, you’d stand up and go
clunk
—you’re one foot shorter. But if the difference was only 0.1 centimeters (1/25 of an inch) you might never know. That’s why I suspect that if my grandmother was right, then the difference is probably only a few centimeters, maybe as much as an inch.
To conduct my experiment, I of course first need to convince them of the uncertainty in my measurements. So I begin by measuring an aluminum rod vertically—it comes to 150.0 centimeters—and I ask them to agree that I’m probably capable of measuring it with an uncertainty of plus or minus one-tenth of a centimeter. So that vertical measurement is 150.0 ± 0.1 centimeters. I then measure the bar when it’s horizontal and come up with 149.9 ± 0.1 centimeters, which is in agreement—within the uncertainty of the measurements—with the vertical measurement.
What did I gain by measuring the aluminum rod in both positions? A lot! For one, the two measurements demonstrate that I was able to
measure length to an accuracy of about 0.1 centimeter (1 millimeter). But at least as important for me is the fact that I want to prove to the students that I’m not playing games with them. Suppose, for example, that I have prepared a specially “cooked” meter stick for my horizontal measurements—that would be a terrible, very dishonest thing to do. By showing that the length of the aluminum rod is the same in the two measurements, I establish that my scientific integrity is beyond doubt.
I then ask for a volunteer, measure him standing up, write that number on the blackboard—185.2 centimeters (or just over 6 feet), plus or minus 0.1 centimeter of course, to account for the uncertainty. Then I help him lie down on my desk in my measuring equipment, which looks like a giant Ritz Stick, the wooden shoe-store foot-measuring device, only his whole body is the foot. I joke back and forth with him about how comfortable he is and congratulate him on his sacrifice for the sake of science, which makes him just a wee bit uneasy. What have I got up my sleeve? I slide the triangular wooden block snug up against his head, and while he lies there, I write the new number on the board. So we now have two measurements, each uncertain by about 0.1 centimeters. What’s the result?
Are you surprised to learn that the two measurements differ by 2.5 centimeters, plus or minus 0.2 centimeters of course? I have to conclude that he is in fact at least 2.3 centimeters (or about 0.9 inches) taller while lying down. I go back to my prone student, announce that he’s roughly an inch taller sleeping than standing up, and—this is the best part—declare, “My grandmother was right! She was always right!”
Are you skeptical? Well, it turns out that my grandmother was a better scientist than most of us. When we are standing, the tug of gravity compresses the soft tissue between the vertebrae of our spines, and when we lie down, our spines expand. This may seem obvious once you know it, but would you have predicted it? In fact, not even the scientists at NASA anticipated this effect in planning the first space missions. The astronauts complained that their suits got tighter when they were in space. Studies done later, during the Skylab mission, showed that of
the six astronauts who were measured, all six showed about 3 percent growth in height—a little over 2 inches if you’re 6 feet tall. Now astronauts’ suits are made with extra room to allow for this growth.
See how revealing good measurements can be? In that same class where I prove my grandmother right, I have a lot of fun measuring some very odd items, all in order to test a suggestion of the great Galileo Galilei, the father of modern science and astronomy, who once asked himself the question, “Why are the largest mammals as large as they are and not much larger?” He answered himself by suggesting that if a mammal became too heavy, its bones would break. When I read about this, I was intrigued to find out whether or not he was right. His answer seemed right intuitively, but I wanted to check it.
I knew that mammals’ femurs—their thighbones—support most of their weight, so I decided to make some comparative measurements of different mammals’ femur bones. If Galileo was right, then for a super heavy mammal, the femur bone would not be strong enough to support the animal. Of course, I realized that the strength of the mammal’s femur should depend on its thickness. Thicker bones can support more weight—that’s intuitive. The bigger the animal, the stronger the bones would need to be.
The femur would also get longer as the animal got bigger, of course, and I realized that by comparing how much longer versus how much thicker the femurs of various mammals get as the animals become bigger, I could test Galileo’s idea. According to the calculations I made, which are more complicated than I want to go into here (I explain them in
appendix 1
), I determined that if Galileo was right, then as mammals get bigger the thickness of their femurs would have to increase faster than their length. I calculated that, for example, if one animal was five times bigger than another—so the femur would be five times longer—then the thickness of its femur would have to be about eleven times greater.
This would mean that at some point the thicknesses of femurs would become the same as their lengths—or even greater—which would make for some pretty impractical mammals. Such an animal would certainly
not be the fittest for survival, and that would then be the reason why there is a maximum limit on the size of mammals.
So, I had my prediction that thickness would increase faster than length. Now the real fun began.
I went over to Harvard University, where they have a beautiful collection of bones, and I asked them for the femurs of a raccoon and a horse. It turns out that a horse is about four times larger than a raccoon, and sure enough, the horse’s femur (42.0 ± 0.5 centimeters) was about three and a half times longer than the raccoon’s (12.4 ± 0.3 centimeters). So far so good. I plugged the numbers into my formula and predicted that the horse’s femur should be a little more than six times thicker than the raccoon’s. When I measured the thicknesses (to an uncertainty of about half a centimeter for the raccoon and 2 centimeters for the horse), it turned out that the horse bone was five times thicker, plus or minus about 10 percent. So it looked very good for Galileo. However, I decided to expand the data to include smaller as well as larger mammals.
So I went back to Harvard, and they gave me three more bones, of an antelope, an opossum, and a mouse. Here’s how they all stacked up:
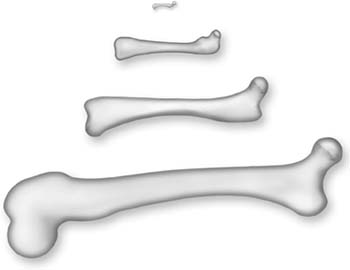
Isn’t that wonderful, so romantic? The progression of shapes is lovely, and look at how delicate, how tiny is the femur of the mouse. Only a teeny weenie little femur for a teeny, weenie little mouse. Isn’t that beautiful? I will never cease to be amazed by the beauty in every detail of our natural world.
But what about the measurements; how did they fit into my equation? When I did the calculations, I was shocked, really shocked. The horse femur is about 40 times longer than the mouse’s, and my calculations predicted that its femur should be more than 250 times thicker. Instead, it was only about 70 times thicker.
So I said to myself, “Why didn’t I ask them for the femur of an elephant? That might settle the issue conclusively.” I think they were somewhat annoyed at Harvard when I came back again, but they kindly gave me the femur of an elephant. By that time I’m sure they just wanted to get rid of me! Believe me, it was difficult carrying that bone; it was more than a yard long and weighed a ton. I couldn’t wait to do my measurements; I couldn’t sleep all night.
And do you know what I found? The mouse’s femur was 1.1 ± 0.05 centimeters long and 0.7 ± 0.1 millimeters thick—very thin indeed. The elephant’s femur was 101 ± 1 centimeters long, about 100 times longer than that of the mouse. So how about its thickness? I measured it at 86 ± 4 millimeters, roughly 120 times the diameter of the mouse’s femur. But according to my calculations, if Galileo was right, the femur of the elephant should be roughly 1,000 times thicker than that of the mouse. In other words, it should have been about 70 centimeters thick. Instead, the actual thickness was only about 9 centimeters. I concluded, however reluctantly, that the great Galileo Galilei was wrong!
Measuring Interstellar Space
One of the areas of physics in which measurement has been bedeviling is astronomy. Measurements and uncertainties are enormous issues for astronomers, especially because we deal with such immense distances.
How far away are the stars? How about our beautiful neighbor, the Andromeda Galaxy? And what about all the galaxies we can see with the most powerful telescopes? When we see the most-distant objects in space, how far are we seeing? How large is the universe?
These are some of the most fundamental and profound questions in all of science. And the different answers have turned our view of the universe upside down. In fact, the whole distance business has a wonderful history. You can trace the evolution of astronomy itself through the changing techniques of calculating stellar distances. And at every stage these are dependent on the degree of accuracy of measurements, which is to say the equipment and the inventiveness of astronomers. Until the end of the nineteenth century, the only way astronomers could make these calculations was by measuring something called parallax.
You are all familiar with the phenomenon of parallax without even realizing it. Wherever you are sitting, look around and find a stretch of wall with some sort of feature along it—a doorway or a picture hanging on it—or if you’re outside some feature of the landscape, like a big tree. Now stretch your hand straight out in front of you and raise one finger so that it is to one or the other side of that feature. Now first close your right eye and then close your left eye. You will see that your finger jumped from left to right relative to the doorway or the tree. Now, move your finger closer to your eyes and do it again. Your finger moves even more. The effect is
huge
! This is parallax.
