For the Love of Physics (11 page)
Read For the Love of Physics Online
Authors: Walter Lewin
Tags: #Biography & Autobiography, #Science & Technology, #Science, #General, #Physics, #Astrophysics, #Essays

To bring the equation to a much more careful test than what I did with the handheld small apple pendulum, I had a simple pendulum constructed in my classroom: a rope 5.18 meters (about 17 feet) long with
a spherical steel bob weighing 15 kilograms at the end of the rope. I call it the mother of all pendulums. You can see it near the end of my lecture here:
http://ocw.mit.edu/courses/physics/8-01-physics-i-classical-mechanics-fall-1999/video-lectures/embed10/
.
What should the period,
T
, of this pendulum be?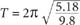 , which is 4.57 seconds. To bring this to a test, as I promised my students, I measure the period both for a 5-degree and for a 10-degree amplitude.
, which is 4.57 seconds. To bring this to a test, as I promised my students, I measure the period both for a 5-degree and for a 10-degree amplitude.
I use a large digital timer that the students can see, and that displays the time to an accuracy of one-hundredth of a second. I’ve tested my reaction time in turning the timer on and off countless times over the years, and I know it’s about one-tenth of a second (on a good day). This means that if I repeat the very same measurement a dozen times I will get measurements for the period that will vary by as much as 0.1 (maybe 0.15) seconds. So whether I measure the time it takes for one oscillation or for ten oscillations, my timing will have an uncertainty of plus or minus 0.1 seconds. I therefore let the pendulum swing ten times, as that will give a ten times more accurate value for the period than if I let it swing only once.
I pull the bob out enough so that the angle of the rope with the vertical is about 5 degrees and then let it go and start the timer. The class counts each of the swings out loud, and after ten oscillations I stop the timer. It’s amazing—the timer reads 45.70 seconds, ten times my estimate for one swing. The class applauds wildly.
Then I increase the amplitude to 10 degrees, let the bob go, start the timer, get the class counting, and right at ten, I stop the timer: 45.75 seconds. 45.75 ± 0.1 seconds for ten oscillations translates into 4.575 ± 0.01 seconds per oscillation. The result for the 5-degree amplitude is the same as for the 10-degree amplitude (within the uncertainty of the measurements). So my equation is still very accurate.
Then I ask the class, Suppose I sat on the bob and swung along with it—would we get the same period, or would it change? I never look forward to sitting on this thing (it really hurts), but for science, and to get the students laughing and involved, I wouldn’t miss the opportunity. Of
course I can’t sit upright on the bob because that way I will effectively shorten the rope, and reduce the period a bit. But if I make my body as horizontal as possible in order to be at the same level as the bob, I keep the rope length pretty much the same. So I pull the bob up, put it between my legs, grasp the rope, and let myself go. You can see this on the jacket of this book!
It’s not easy for me to start and stop the timer while hanging on the pendulum without increasing my reaction time. However, I’ve practiced this so many times that I am quite sure that I can achieve an uncertainty in my measurements of ± 0.1 seconds. I swing ten times, with students counting the swings out loud—and laughing at the absurdity of my situation while I complain and groan loudly—and when after ten oscillations I turn off the timer, it reads 45.61 seconds. That’s a period of 4.56 ± 0.01 seconds. “Physics works!” I scream, and the students go bananas.
Grandmothers and Astronauts
Another tricky aspect of gravity is that we can be fooled into perceiving that it’s pulling from a different direction than it really is. Gravity always pulls toward the center of Earth—on Earth, that is, not on Pluto of course. But we can sometimes perceive that gravity is operating horizontally, and this artificial or perceived gravity, as we call it, can in fact seem to defy gravity itself.
You can demonstrate this artificial gravity easily by doing something my grandmother used to do every time she made a salad. My grandmother had such fantastic ideas—remember, she’s the one who taught me that you’re longer when you’re lying down than when you’re standing up. Well, when she made a salad, she really had a good time. She would wash the lettuce in a colander, and then rather than drying it in a cloth towel, which would damage the leaves, she had invented her own technique: she took the colander and put a dish towel over the top, holding it in place with a rubber band, and then she would swing it around furiously in a circle—I mean really fast.
That’s why when I demonstrate this in class, I make sure to tell the students in the first two rows to close their notebooks so their pages don’t get wet. I bring lettuce into the classroom, wash it carefully in the sink on my table, prepare it in the colander. “Get ready,” I tell them, and I swing my arm vigorously in a vertical circle. Water drops spray everywhere! Now, of course, we have boring plastic salad spinners to substitute for my grandmother’s method—a real pity in my book. So much of modern life seems to take the romance out of things.
This same artificial gravity is experienced by astronauts as they accelerate into orbit around the Earth. A friend and MIT colleague of mine, Jeffrey Hoffman, has flown five missions in the space shuttle, and he tells me that the crew experiences a range of different accelerations in the course of a launch, from about 0.5
g
initially, building to about 2.5
g
at the end of the solid fuel stage. Then it drops back down to about 1
g
briefly, at which point the liquid fuel starts burning, and acceleration builds back up to 3
g
for the last minute of the launch—which takes about eight and a half minutes total to obtain a speed of about 17,000 miles per hour. And it’s not at all comfortable. When they finally reach orbit they become weightless and they perceive this as zero gravity.
As you now know, both the lettuce, feeling the colander pushing against it, and the astronauts, feeling the seats pushing against them, are experiencing a kind of artificial gravity. My grandmother’s contraption—and our salad spinners—are of course versions of a centrifuge, separating the lettuce from the water clinging to its leaves, which shoots out through the colander’s holes. You don’t have to be an astronaut to experience this perceived gravity. Think of the fiendish ride at amusement parks called the Rotor, in which you stand at the edge of a large rotating turntable with your back against a metal fence. As it starts to rotate faster and faster, you feel more and more pushed into the fence, right? According to Newton’s third law, you push on the wall with the same force as the wall pushes on you.
This force with which the wall pushes on you is called the centripetal
force. It provides the necessary acceleration for you to go around; the faster you go, the larger is the centripetal force. Remember, if you go around in a circle, a force (and therefore an acceleration) is required even if the speed remains unchanged. In similar fashion, gravity provides the centripetal force on planets to go around the Sun, as I discuss in
appendix 2
. The force with which you push on the wall is often called the centrifugal force. The centripetal force and the centrifugal force have the same magnitude but in opposite direction. Do not confuse the two. It’s
only
the centripetal force that acts on you (not the centrifugal force), and it is only the centrifugal force that acts on the wall (not the centripetal force).
Some Rotors can go so fast that they can lower the floor on which you stand and you won’t slide down. Why won’t you slide down?
Think about it. If the Rotor isn’t spinning at all the force of gravity on you will make you slide down as the frictional force between you and the wall (which will be upward) is not large enough to balance the force of gravity. However, the frictional force, with the floor lowered, will be higher when the Rotor spins, as it depends on the centripetal force. The larger the centripetal force (with the floor lowered), the larger the frictional force. Thus, if the Rotor spins fast enough with the floor lowered, the frictional force can be large enough that it will balance the force of gravity and thus you won’t slide down.
There are lots of ways to demonstrate artificial gravity. Here’s one you can try at home; well, in your backyard. Tie a rope to the handle of an empty paint can and fill the can with water—about half full, I’d say, otherwise it will be awfully heavy to spin—and then whip the can around as hard as you can up over your head in a circle. It might take some practice to get it going fast enough. Once you do, you’ll see that not a drop of water will fall out. I have students do this in my classes, and I must say it’s a complete riot! This little experiment also explains why, with some especially pernicious versions of the Rotor, it will gradually turn over until you are completely upside down at one point, and yet you
don’t drop down to the ground (of course, for safety’s sake, you are also strapped into the thing).
The force with which a scale pushes on us determines what the scale tells us we weigh; it’s the force of gravity—not the lack of it—that makes astronauts weightless; and when an apple falls to Earth, the Earth falls to the apple. Newton’s laws are simple, far-reaching, profound, and utterly counterintuitive. In working out his famous laws, Sir Isaac Newton was contending with a truly mysterious universe, and we have all benefited enormously from his ability to unlock some of these mysteries and to make us see our world in a fundamentally new way.
CHAPTER 4

The Magic of Drinking with a Straw
O
ne of my favorite in-class demonstrations involves two paint cans and a rifle. I fill one can to the rim with water and then bang the top on tightly. Then I fill the second can most of the way, but leaving an inch or so of space below the rim, and also seal that one. After placing them one in front of the other on a table, I walk over to a second table several yards away, on which rests a long white wooden box, clearly covering some kind of contraption. I lift up the box, revealing a rifle fastened onto a stand, pointing at the paint cans. The students’ eyes widen—am I going to fire a rifle in class?
“If we were to shoot a bullet through these paint cans, what would happen?” I ask them. I don’t wait for answers. I bend down to check the rifle’s aim, usually fiddling with the bolt a little. This is good for building up tension. I blow some dust out of the chamber, slide a bullet in, and announce, “All right, there goes the bullet. Are we ready for this?” Then standing alongside the rifle, I put my finger on the trigger, count “Three, two, one”—and fire. One paint can’s top instantly pops way up into the air, while the other one stays put. Which can do you think loses its top?
To know the answer, you first have to know that air is compressible
and water isn’t; air molecules can be squished closer in toward one another, as can the molecules of any gas, but those of water—and of any liquid at all—cannot. It takes horrendous forces and pressures to change the density of a liquid. Now, when the bullet enters the paint cans, it brings a great deal of pressure with it. In the can with the air in it, the air acts like a cushion, or a shock absorber, so the water isn’t disturbed and the can doesn’t explode. But in the can full of water, the water can’t compress. So the extra pressure the bullet introduces in the water exerts a good deal of force on the walls and on the top of the can and the top blows off. As you may imagine, it’s really very dramatic and my students are always quite shocked.
Surrounded by Air Pressure
I always have a lot of fun with pressure in my classes, and air pressure is particularly entertaining because so much is so counterintuitive about it. We don’t even realize we are experiencing air pressure until we actually look for it, and then it’s just astonishing. Once we realize it’s there—and begin to understand it—we begin to see evidence for it everywhere, from balloons to barometers, to why a drinking straw works, to how deep you can swim and snorkel in the ocean.
The things we don’t see at first, and take for granted, like gravity and air pressure, turn out to be among the most fascinating of all phenomena. It’s like the joke about two fish swimming along happily in a river. One fish turns to the other, a skeptical look on its face, and says, “What’s all this new talk about ‘water’?”
